Lý thuyết Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh từ đó chứng minh tính chất khác

- Để chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh ta làm theo các bước:

+ Xét hai tam giác;

+ Kiểm tra hai cặp cạnh bằng nhau và cặp góc xen giữa hai cạnh đó bằng nhau;

+ Kết luận hai tam giác bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).

- Sử dụng trường hợp bằng nhau cạnh – góc – cạnh để chứng minh các cạnh, các góc bằng nhau, tính độ dài cạnh và số đo góc ta làm theo các bước:

+ Xác định hai tam giác có các cạnh (hoặc góc) cần chứng minh bằng nhau hoặc cạnh cần tính độ dài hay góc cần tính số đo;

+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh;

+ Suy ra các cạnh, các góc tương ứng bằng nhau hoặc độ dài cạnh hay số đo góc cần tính.

Ngoài ra kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, tổng ba góc trong một tam giác,…để suy ra những khẳng định đúng.

Ví dụ 1. Qua trung điểm I của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB, trên đường thẳng vuông góc đó lấy hai điểm C và D. Nối CA, CB, DA, DB. Tìm các cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.

Hướng dẫn giải

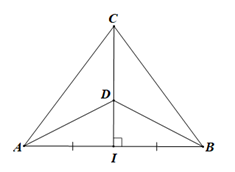
Vì C nằm trên đường thẳng vuông góc với AB tại I nên ta có: \(\widehat {CIA} = \widehat {CIB} = 90^\circ \)

Vì D nằm trên đường thẳng vuông góc với AB tại I nên ta có: \[\widehat {DIA} = \widehat {DIB} = 90^\circ \]

+) Xét tam giác ADI và tam giác BDI có:

DI là cạnh chung,

\[\widehat {DIA} = \widehat {DIB}\left( { = 90^\circ } \right)\] (chứng minh trên),

AI = BI (do I là trung điểm của AB),

Do đó DADI = DBDI (c.g.c)

+) Xét tam giác ACI và tam giác BCI có:

CI là cạnh chung,

\[\widehat {CIA} = \widehat {CIB}\left( { = 90^\circ } \right)\] (chứng minh trên),

AI = BI (do I là trung điểm của AB),

Do đó DACI = DBCI (c.g.c)

Suy ra AC = BC (hai cạnh tương ứng) và \(\widehat {ACI} = \widehat {BCI}\) (hai góc tương ứng)

+) Xét tam giác ACD và tam giác BCD có:

AC = BC (chứng minh trên),

\(\widehat {ACD} = \widehat {BCD}\) (do \(\widehat {ACI} = \widehat {BCI}\)),

CD là cạnh chung

Do đó DACD = DBCD (c.g.c).

Hướng dẫn giải

Ví dụ 2. Cho tam giác nhọn ABC, M là trung điểm của BC. Đường thẳng vuông góc với AB tại B cắt đường thẳng AM tại D. Trên tia MA lấy điểm E sao cho ME = MD. CE cắt AB tại K. Chứng minh:

a) DEMC = DDMB;

b) DAKE vuông tại K.

Hướng dẫn giải

Chứng minh (Hình vẽ dưới đây):

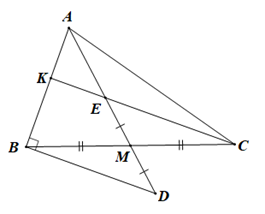
a) Xét tam giác EMC và tan giác DMB có:

ME = MD (giả thiết),

\(\widehat {EMC} = \widehat {DMB}\) (hai góc đối đỉnh),

MB = MC (do M là trung điểm của BC)

Do đó DEMC = DDMB (c.g.c)

Vậy DEMC = DDMB.

b) Vì DEMC = DDMB (chứng minh câu a)

Suy ra \(\widehat {CEM} = \widehat {BDM}\) (hai góc tương ứng)

Lại có \(\widehat {CEM} = \widehat {AEK}\) (hai góc đối đỉnh)

Nên \(\widehat {AEK} = \widehat {BDM} = \widehat {BDA}\)

Mà \(\widehat {BDA} + \widehat {BAD} = 90^\circ \) (trong tam giác ABD vuông tại B, hai góc nhọn phụ nhau)

Do đó \(\widehat {AEK} + \widehat {KAE} = 90^\circ \)

Xét tam giác AKE có: \(\widehat {AEK} + \widehat {KAE} + \widehat {AKE} = 180^\circ \) (tổng ba góc trong một tam giác)

Suy ra \(\widehat {AKE} = 180^\circ  - \left( {\widehat {AEK} + \widehat {KAE}} \right)\)

Hay \(\widehat {AKE} = 180^\circ  - 90^\circ  = 90^\circ \)

Vậy tam giác AKE vuông tại K.