Lý thuyết Áp dụng công thức tính diện tích xung quanh và thể tích để giải các bài toán thực tế
Trong thực tế đời sống, chúng ta dễ gặp các hình như hộp đựng quà, bể cá cảnh, chiếc đèn lồng, khối rubik, … đó là những hình ảnh về hình lăng trụ đứng.
Để tính được thể tích hay để làm những đồ vật này cần bao nhiêu (diện tích) vật liệu thì hợp lí, ta sẽ sử dụng các công thức đã được học như:
- Công thức tính chu vi, diện tích các hình học cơ bản: tam giác, hình vuông, hình chữ nhật, hình thang, hình bình hành, hình thoi,…
- Công thức tính diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác (tứ giác).
Ví dụ 1. Một quyển lịch để bàn gồm các tờ lịch được đặt trên một giá đỡ bằng bìa có dạng hình lăng trụ đứng tam giác kích thước như hình vẽ.
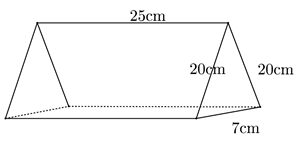
Tính diện tích bìa dùng để làm giá đỡ của quyển lịch.
Hướng dẫn giải
Diện tích bìa dùng để làm giá đỡ của quyển lịch là diện tích xung quanh của hình lăng trụ đứng tam giác.
Khi đó:
Sxq = C. h = (20 + 20 + 7). 25 = 47. 25 = 1 175 (cm2)
Vậy diện tích bìa cần dùng là 1 175 cm2.
Ví dụ 2. Một khối kim loại có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Tính thể tích của khối kim loại vuông (m3) (không tính cái lỗ) biết khối kim loại dài 0,45 m.
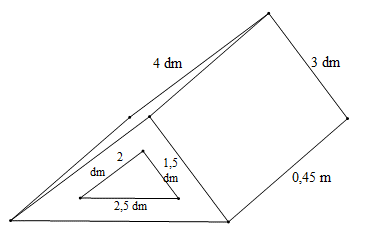
Hướng dẫn giải
Đổi 3 dm = 30 cm; 4 dm = 40 cm; 5 dm = 50 cm;
1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm;
0,45 m = 45 cm.
Thể tích của khối kim loại bao gồm cả lỗ là:
V = (12. 40. 30). 45 = 27 000 (cm3) = 0,027 (m3)
Thể tích của phần lỗ bị khoét đi là:
V' = (12. 20. 15) . 45 = 6 750 (cm3) = 0,00675 (m3)
Thể tích của khối kim loại là:
0,027 – 0,00675 = 0,02025 (m3).
Vậy thể tích của khối kim loại đặc đó là 0,02025 m3.