Lý thuyết Xác định loại tam giác dựa vào số đo góc của tam giác đó

Để xác định được một tam giác là tam giác nhọn, tam giác vuông hay tam giác tù, ta dựa vào số đo các góc của tam giác đó.

Ta thực hiện các bước sau:

Bước 1: Tính số đo các góc của tam giác

Bước 2: Xác định góc trong tam giác là góc gì

Ta sẽ so sánh số đo góc với 90°:

+ Góc nhọn: là góc có số đo nhỏ hơn 90°;

+ Góc vuông: là góc có số đo bằng 90°;

+ Góc tù: là góc có số đo lớn hơn 90°;

Bước 3: Xác định tam giác dựa vào số đo các góc

+ Tam giác có ba góc nhọn là tam giác nhọn;

+ Tam giác có một góc vuông là tam giác vuông;

+ Tam giác có một góc tù là tam giác tù.

Ví dụ 1. Xác định trong các tam giác dưới đây, tam giác nào tam giác nhọn, tam giác vuông, tam giác tù?

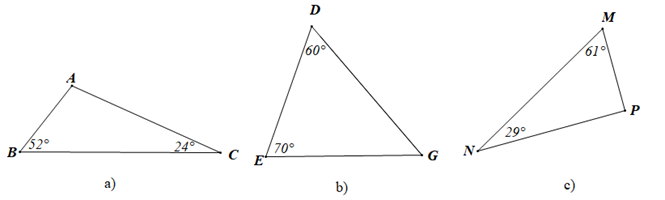
Hướng dẫn giải

a) Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat A = 180^\circ  - \widehat B - \widehat C\)

Hay \(\widehat A = 180^\circ  - 52^\circ  - 24^\circ  = 104^\circ \)

Ta thấy 104° > 90° nên góc A là góc tù.

Vậy tam giác ABC là tam giác tù.

b) Xét tam giác DEG có \(\widehat D + \widehat E + \widehat G = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat G = 180^\circ  - \widehat D - \widehat E\)

Hay \(\widehat G = 180^\circ  - 60^\circ  - 70^\circ  = 50^\circ \)

Ta thấy 50° < 60° < 70° < 90°

Do đó ba góc của tam giác DEG đều là góc nhọn.

Vậy tam giác DEG là tam giác nhọn.

c) Xét tam giác MNP có \(\widehat M + \widehat N + \widehat P = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat P = 180^\circ  - \widehat M - \widehat N\)

Hay \(\widehat P = 180^\circ  - 61^\circ  - 29^\circ  = 90^\circ \)

Do đó góc P là góc vuông

Vậy tam giác MNP là tam giác vuông tại P.

Ví dụ 2. Cho tam giác vuông tại A, kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác góc C và \(\widehat {BAH}\) cắt nhau tại I. Tam giác IAC là tam giác gì? Vì sao?

Hướng dẫn giải

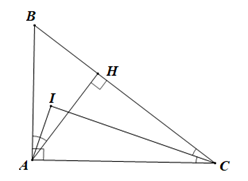
Xét tam giác ABC vuông tại A (giả thiết) nên ta có \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) (trong tam giác vuông hai góc nhọn phụ nhau)

Hay \(\widehat {ABH} + \widehat {ACH} = 90^\circ \)            

Suy ra \(\widehat {ACH} = 90^\circ  - \widehat {ABH}\) (1)

Vì AH ^ BC (giả thiết) nên tam giác ABH vuông tại H,

Do đó \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (trong tam giác vuông hai góc nhọn phụ nhau)

Hay \(\widehat {BAH} = 90^\circ  - \widehat {ABH}\)              (2)

Từ (1) và (2) ta có: \(\widehat {ACH} = \widehat {BAH}\) (cùng phụ với \(\widehat {ABH}\))

Mà AI là tia phân giác của \(\widehat {BAH}\) (giả thiết) nên \(\widehat {BAI} = \frac{1}{2}\widehat {BAH}\) (tính chất tia phân giác của một góc)

CI là tia phân giác của \(\widehat {ACB}\) (giả thiết) nên \(\widehat {ACI} = \frac{1}{2}\widehat {ACB} = \frac{1}{2}\widehat {ACH}\) (tính chất tia phân giác của một góc)

Do đó \(\widehat {BAI} = \widehat {ACI}\)

Xét tam giác IAC có \(\widehat {IAC} + \widehat {ACI} + \widehat {AIC} = 180^\circ \) (tổng ba góc trong một tam giác)

Hay \(\widehat {IAC} + \widehat {BAI} + \widehat {AIC} = 180^\circ \) (do \(\widehat {BAI} = \widehat {ACI}\))

Suy ra \(\widehat {BAC} + \widehat {AIC} = 180^\circ \)

Suy ra \(\widehat {AIC} = 180^\circ  - \widehat {BAC}\)

Mà \(\widehat {BAC} = 90^\circ \) do đó \(\widehat {AIC} = 180^\circ  - 90^\circ  = 90^\circ \)

Do đó tam giác IAC là tam giác vuông tại I.