Lý thuyết Thứ tự trong tập số thực và biểu diễn số thực trên trục số
* Để biết được thứ tự trong tập số thực thì ta cần so sánh các số thực với nhau từ đó suy ra thứ tự của chúng.
Để so sánh được các số thực ta cần nắm vững:
–Với hai số thực x, y bất kỳ, ta luôn có x = y hoặc x < y hoặc x > y.
– Các số thực lớn hơn 0 gọi là số thực dương, các số thực nhỏ hơn 0 gọi là các số thực âm. Số 0 không là số thực dương cũng không là số thực âm.
– Việc so sánh các số thực dương làm tương tự như so sánh các số hữu tỉ.
– Với a,b là hai số thực dương, nếu a > b thì \(\sqrt a > \sqrt b \).
Khi đó thứ tự của hai số thực a và b là:
– Nếu a > b thì a đứng sau b trong tập số thực.
– Ngược lại nếu a < b thì a đứng trước b trong tập số thực.
* Ta sẽ biểu diễn được số thực a, b trên trục số khi đã biết thứ tự của chúng trong tập số thực:
– Nếu a > b thì a sẽ nằm về bên phải trục số so với b
– Và ngược lại a < b thì a sẽ nằm về bên trái trục số so với b.
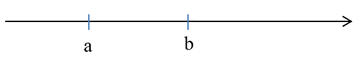
Ví dụ 1: Hãy sắp xếp các số thực sau theo thứ tự tăng dần: \(\sqrt 2 \); \(\sqrt 3 \); \(\sqrt 5 \).
Hướng dẫn giải:
Ta có 2 < 3 < 5 suy ra \(\sqrt 2 < \sqrt 3 < \sqrt 5 \).
Vậy cách sắp xếp theo thứ tự tăng dần là: \(\sqrt 2 \); \(\sqrt 3 \); \(\sqrt 5 \).
Ví dụ 2: Hãy so sánh và biểu diễn thứ tự các số thực sau trên trục số: \(\frac{1}{5}\); \(\frac{1}{{10}}\)
Hướng dẫn giải:
Ta có 10 > 5, nên suy ra \(\frac{1}{{10}} < \frac{1}{5}\).
Biểu diễn trên trục số là:
