Lý thuyết Xác định các cạnh, các góc bằng nhau dựa vào hai tam giác bằng nhau

a) Viết kí hiệu hai tam giác bằng nhau

- Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

- Để kí hiệu bằng nhau của tam giác ABC và tam giác A'B'C' ta viết: DABC = DA'B'C'.

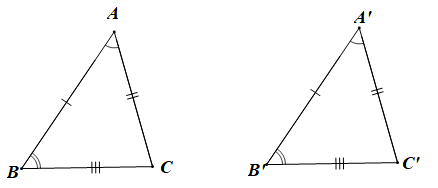
Quy uớc rằng khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo cùng thứ tự.

Khi đó: DABC = DA'B'C' nếu \[\left\{ \begin{array}{l}AB = A'B',BC = B'C',AC = A'C'\\\widehat A = \widehat {A'},\widehat B = \widehat {B'},\widehat C = \widehat {C'}.\end{array} \right.\]

Ở đây:

+ Hai đỉnh A và A' (B và B', C và C') là hai đỉnh tương ứng;

+ Hai góc A và A' (B và B', C và C') là hai góc tương ứng;

+ Hai cạnh AB và A'B' (BC và B'C', AC và A'C') là hai cạnh tương ứng.

b) Từ hai tam giác bằng nhau, xác định các cạnh bằng nhau, các góc bằng nhau và tính độ dài cạnh hoặc số đo góc

Dựa vào quy ước viết các đỉnh tương ứng của hai tam giác bằng nhau theo đúng thứ tự ta được các góc bằng nhau, các cạnh bằng nhau, từ đó ta tính được độ dài cạnh hoặc số đo góc cần tìm.

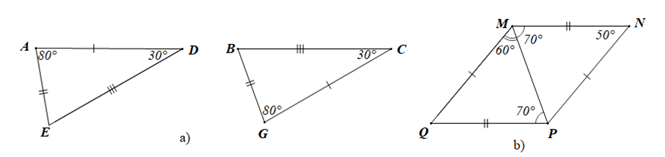
Ví dụ 1. Trong mỗi hình vẽ a) và b) dưới đây, hãy viết kí hiệu bằng nhau của hai tam giác.

Hướng dẫn giải

- Hình vẽ a)

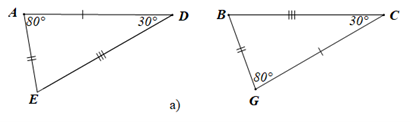
Xét tam giác ADE có \(\widehat A + \widehat D + \widehat E = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat E = 180^\circ  - \widehat A - \widehat D\)

Hay \(\widehat E = 180^\circ  - 80^\circ  - 30^\circ  = 70^\circ \)

Xét tam giác BCG ta cũng có: \(\widehat B + \widehat C + \widehat G = 180^\circ \)(định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat B = 180^\circ  - \widehat C - \widehat G\)

Hay \(\widehat B = 180^\circ  - 30^\circ  - 80^\circ  = 70^\circ \)

Xét tam giác ADE và tam giác BCG có:

+) AD = GC, AE = GB, DE = CB

+) \(\widehat A = \widehat G\left( { = 80^\circ } \right),\widehat D = \widehat C\left( { = 30^\circ } \right),\widehat E = \widehat B\left( { = 70^\circ } \right)\)

Do đó DADE = DGCB.

- Hình vẽ b)

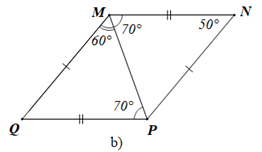
Xét DMNP có \(\widehat {NMP} + \widehat N + \widehat {MPN} = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat {MPN} = 180^\circ  - \widehat {NMP} - \widehat N\)

Hay \(\widehat {MPN} = 180^\circ  - 70^\circ  - 50^\circ  = 60^\circ \)

Xét DMPQ ta có \(\widehat {PMQ} + \widehat Q + \widehat {MPQ} = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat Q = 180^\circ  - \widehat {PMQ} - \widehat {MPQ} = 180^\circ  - 60^\circ  - 70^\circ  = 50^\circ \)

Xét tam giác MNP và tam giác MPQ có:

+) MN = PQ, NP = QM, MP là cạnh chung

+) \(\widehat {NMP} = \widehat {QPM}\left( { = 70^\circ } \right),\widehat N = \widehat Q\left( { = 50^\circ } \right),\widehat {MPN} = \widehat {PMQ}\left( { = 60^\circ } \right)\)

Do đó  DMNP = DPQM.

Ví dụ 2. Cho DABC = DDEG. Biết AB = 4 cm, \(\widehat A = 50^\circ ,\widehat E = 55^\circ .\) Tính độ dài cạnh DE và số đo các góc còn lại của mỗi tam giác.

Hướng dẫn giải

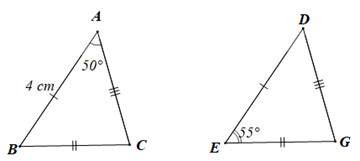
- Vì DABC = DDEG nên ta có:

+) AB = DE (hai cạnh tương ứng)

Mà AB = 4 cm nên DE = 4cm;

+) \(\widehat A = \widehat D,\widehat B = \widehat E,\widehat C = \widehat G\) (các cặp góc tương ứng)

Mà \(\widehat A = 50^\circ ,\widehat E = 55^\circ \) nên \(\widehat D = 50^\circ ,\widehat B = 55^\circ \)

- Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat C = 180^\circ  - \widehat A - \widehat B\)

Hay \(\widehat G = \widehat C = 180^\circ  - 50^\circ  - 55^\circ  = 75^\circ \)

Vậy DE = 4 cm và \(\widehat B = 55^\circ ,\widehat C = \widehat G = 75^\circ ,\widehat D = 50^\circ .\)