ĐGNL ĐH Bách khoa - Vấn đề thuộc lĩnh vực vật lí - Đại cương về dao động điều hòa
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
A. Biên độ, tần số.
B. Biên độ, gia tốc.
C. Vận tốc, tần số.
D. Li độ, vận tốc.
A. Biên độ dao động
B. Trạng thái dao động
C. Tần số dao động
D. Chu kỳ dao động
A. Cách chọn gốc tọa độ và gốc thời gian
B. Năng lượng truyền cho vật để vật dao động
C. Đặc tính của hệ dao động
D. Cách kích thích vật dao động
Một vật dao động điều hoà dọc theo trục Ox với phương trình: x = Acos(πt) cm. Nếu chọn gốc toạ độ O tại vị trí cân bằng của vật thì gốc thời gian t=0 là lúc vật:
A. Ở vị trí li độ cực đại thuộc phần dương của trục Ox
B. Qua vị trí cân bằng O ngược chiều dương của trục Ox
C. Ở vị trí li độ cực đại thuộc phần âm của trục Ox
D. Qua vị trí cân bằng O theo chiều dương của trục Ox
A. Vật chuyển động nhanh dần đều
B. Vật chuyển động chậm dần đều
C. Gia tốc cùng hướng với chuyển động
D. Gia tốc có độ lớn tăng dần
A. Vật đang chuyển động nhanh dần đều theo chiều dương
B. Vật đang chuyển động nhanh dần về vị trí cân bằng
C. Vật đang chuyển động chậm dần theo chiều âm
D. Vật đang chuyển động chậm dần về biên
A. Biên độ của dao động bằng bán kính quỹ đạo của chuyển động tròn đều
B. Vận tốc của dao động bằng vận tốc dài của chuyển động tròn đều
C.Tần số góc của dao động bằng tốc độ góc của chuyển động tròn đều
D. Li độ của dao động bằng toạ độ hình chiếu của chuyển động tròn đều
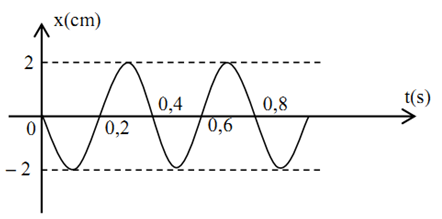
A. A = 2cm, T = 0,8s
B. A = 4cm, T = 0,4s
C. A = 2cm, T = 0,4s
D. A = 4cm, T = 0,8s
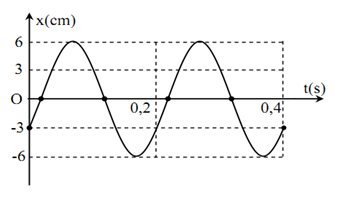
A. vmax= 30πcm/s
B. vmax= 60πcm/s
C. vmax= 60cm/s
D. vmax= 30cm/s
Vật dao động điều hòa có đồ thị vận tốc - thời gian như hình vẽ. Tần số góc và pha ban đầu của li độ của vật là:
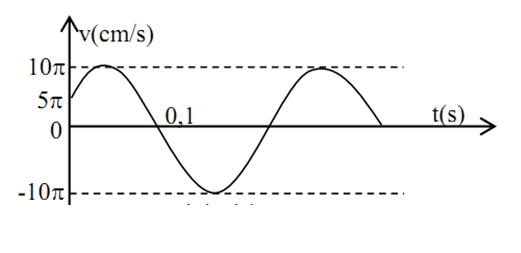
A. \[\omega = \frac{{25\pi }}{3},\varphi = - \frac{\pi }{6}\]
B. \[\omega = \frac{{25\pi }}{3},\varphi = \frac{{7\pi }}{6}\]
C. \[\omega = \frac{{10\pi }}{3},\varphi = \frac{\pi }{3}\]
D.\[\omega = \frac{{10\pi }}{3},\varphi = \frac{\pi }{2}\]Trả lời:
Một con lắc lò xo dao động với phương trình x = 6cos(20πt)cm. Xác định chu kỳ, tần số dao động của chất điểm.
A. f = 10Hz; T = 0,1s
B. f = 1Hz; T = 1s
C. f = 100Hz; T = 0,01s
D. f = 5Hz; T = 0,2s
Một chất điểm dao động điều hoà với phương trình dạng
\[x = 5\cos \left( {7\pi t + \frac{{7\pi }}{6}} \right)cm\]. Biểu thức vận tốc tức thời của chất điểm là:
A. \[v = 5\sin \left( {7\pi t + \frac{{7\pi }}{6}} \right)cm/s\]
B. \[v = 5\cos \left( {7\pi t + \frac{{5\pi }}{3}} \right)cm/s\]
C. \[v = 35\pi \sin \left( {7\pi t + \frac{{7\pi }}{6}} \right)cm/s\]
D. \[v = 35\cos \left( {7\pi t + \frac{{5\pi }}{3}} \right)cm/s\]
Một vật dao động điều hoà chu kỳ T. Gọi vmax và amax tuơng ứng là vận tốc cực đại và gia tốc cực đại của vật. Hệ thức liên hệ sai giữa vmax và amax là:
A. \[\frac{{{a_{\max }}}}{{{v_{\max }}}} = \omega \]
B. \[\frac{{{a_{\max }}}}{{{v^2}_{\max }}} = \frac{1}{A}\]
C. \[\frac{{{a^2}_{\max }}}{{{v_{\max }}}} = A\]
D. \[\frac{{{a_{\max }}}}{{{v_{\max }}}} = \frac{{2\pi }}{T}\]
Một vật dao động điều hòa có biên độ là 2(cm) và tần số góc \[\omega = 2\pi \left( {rad} \right)\]. Lấy \[{\pi ^2} = 10\], gia tốc của vật tại thời điểm vật có vận tốc \[v = 2\sqrt 3 \pi cm/s\]là:
A.40cm/s2
B.80cm/s2
C.±40cm/s2
Một chất điểm dao động điều hoà với phương trình dạng
\[x = \cos \left( {2\pi t + \frac{\pi }{6}} \right)\left( {cm,s} \right)\]. Lấy π2 = 10, biểu thức gia tốc tức thời của chất điểm là:
A. a = 20sin(2πt + π/6) cm/s2
B. a = 40sin(2πt + π/6) cm/s2
C. a = -40cos(2πt + π/6) cm/s2
D. a = 2πsin(2πt + π/6) cm/s2
Một vật thực hiện dao động điều hòa trên đoạn thẳng dài 12cm. Thời gian để vật đi được đoạn đường dài 24cm là 2s. Tốc độ của vật khi đi qua vị trí cân bằng là
A. 3πcm/s.
B. 6π cm/s.
C. 12πcm/s.
D. 24πcm/s.
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
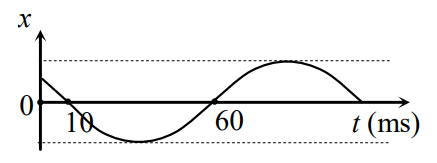
A. 0,06 s.
B. 0,12 s.
C. 0,1 s.
D. 0,05 s.
Một đĩa phẳng nhẵn nằm ngang, chuyển động tròn đều với vận tốc góc ωω quanh trục thẳng đúng đi qua tâm của đĩa. Trên đĩa có một thanh mảnh đồng chất AB có thể quay tự do quanh trục được gắn chặt với đĩa và đi qua đầu A của thanh. Khi thanh AB đang ở vị trí như hình vẽ, tác động nhẹ vào đầu B của thanh để thanh AB quay với vận tốc góc ban đầu ω0ω0 so với đĩa (ω0ω0khá nhỏ so với ωω). Người ta quan sát đứng trên đĩa sẽ thấy thanh chuyển động như thế nào?
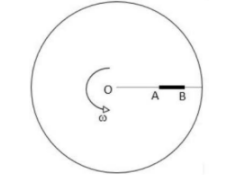
A. Thanh quay đi một góc rồi dừng lại.
B. Thanh quay tròn.
C. Thanh dao động quanh vị trí cân bằng.
D. Chuyển động của thanh có dạng phức tạp hơn các trường hợp trên.