Góc giữa đường thẳng và mặt phẳng trong không gian

Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với Sinx

1Làm xong biết đáp án, phương pháp giải chi tiết.
2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
4Biết điểm yếu và có hướng giải pháp cải thiện

Bắt đầu luyện tập

Số câu đúng

0/15

Thời gian làm bài

00:00:00

Số câu đã làm

Câu 1:

Cho tứ diện ABCD có cạnh AB, BC, CD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?

A. Góc giữa AC và (BCD) là góc ACB.

B. Góc giữa AD và (ABC) là góc ADB.

C. Góc giữa AC và (ABD) là góc CAB.

D. Góc giữa CD và (ABD) là góc CBD.

Câu 2:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC=a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB=a. Tính số đo của góc giữa SA và (ABC).

A. $30^{°}$

B. $45^{°}$

C. $60^{°}$

D. $75^{°}$

Câu 3:

Cho tam giác ABC vuông cân tại A và BC=a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm SS sao cho

S A = \frac{a \sqrt{6}}{2}

. Tính số đo góc giữa đường thẳng SA và (ABC)

A. $30^{°}$

B. $45^{°}$

C. $60^{°}$

D. $90 °$

Câu 4:

Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng aa và

S A ⊥ (A B C D) .

Biết

S A = \frac{a \sqrt{6}}{3}

. Tính góc giữa SC và (ABCD).

A. $30^{°}$

B. $45^{°}$

C. $60^{°}$

D. $75^{°}$

Câu 5:

Cho hình lập phương

A B C D . A_{1} B_{1} C_{1} D_{1}

. Gọi αα là góc giữa AC₁ và mp(ABCD). Chọn khẳng định đúng trong các khẳng định sau?

A. $α = 45^{0}$

B. $\tan α = \frac{1}{\sqrt{2}}$

C. $\tan α = \frac{2}{\sqrt{3}}$

D. $α = 30^{0}$

Câu 6:

Cho hình chóp S.ABCD có

S A ⊥ (A B C D)

và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD và I là trung điểm của SC. Khẳng định nào sau đây sai ?

A. $I O ⊥ (A B C D) .$

B. $B C ⊥ S B .$

C. (SAC) là mặt phẳng trung trực của đoạn BD.

D. Tam giác SCD vuông ở D.

Câu 7:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm

Δ A B C

. Độ dài SG là:

A. $\frac{\sqrt{9 b^{2} + 3 a^{2}}}{3}$

B. $\frac{\sqrt{b^{2} - 3 a^{2}}}{3}$

C. $\frac{\sqrt{9 b^{2} - 3 a^{2}}}{3}$

D. $\frac{\sqrt{b^{2} + 3 a^{2}}}{3}$

Câu 8:

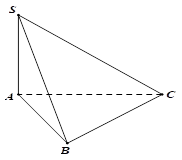
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a,BC=2a, SA vuông góc với mặt phẳng đáy và

S A = \sqrt{15} a

(tham khảo hình bên). Góc giữa đường thẳng SC và mặt phẳng đáy bằng

A. $90^{\circ}$

B. $45^{\circ}$

C. $30^{\circ}$

D. $60^{\circ}$

Câu 9:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).

A. $60^{0}$

B. $75^{0}$

C. $45^{0}$

D. $30^{0}$

Câu 10:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,

S A ⊥ (A B C D), S A = a \sqrt{6}

. Gọi

α

là góc giữa SC và mp(SAB). Chọn khẳng định đúng trong các khẳng định sau?

A. $\tan α = \frac{1}{\sqrt{8}} .$

B. $\tan α = \frac{1}{\sqrt{7}} .$

C. $α = 30^{0} .$

D. $\tan α = \frac{1}{\sqrt{6}} .$

Câu 11:

Cho hình chóp S.ABCD, với đáy ABCD là hình bình hành tâm O;AD,SA,AB đôi một vuông góc AD=8, SA=6. (P)là mặt phẳng qua trung điểm của AB và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng?

A. 36

B. 16

C. 17

D. 18

Câu 12:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm

Δ A B C

. Xét mặt phẳng (P) đi qua A và vuông góc với SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm C1 nằm giữa S và C.

A. $b > a \sqrt{2}$

B. $b < a \sqrt{2}$

C. $a < b \sqrt{2}$

D. $a > b \sqrt{2}$

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao SH vuông góc với mp(ABCD). Gọi α là góc giữa BD và mp(SAD). Chọn khẳng định đúng trong các khẳng định sau?

A. $α = 60^{0}$

B. $α = 30^{0}$

C. $\cos α = \frac{\sqrt{3}}{2 \sqrt{2}}$

D. $\sin α = \frac{\sqrt{3}}{2 \sqrt{2}}$

Câu 14:

Cho hình thoi ABCD có tâm

O, \hat{A D C} = 60^{0}, A C = 2 a

. Lấy điểm S không thuộc (ABCD) sao cho

S O ⊥ (A B C D) .

Gọi

α

là góc giữa đường thẳng SB và mặt phẳng (ABCD) và

t a n α = \frac{1}{2}

. Gọi

β

là góc giữa SC và (ABCD), chọn mệnh đề đúng :

A. $\sin β = \frac{1}{2}$

B. $\cot β = \frac{\sqrt{3}}{2}$

C. $\tan β = \frac{\sqrt{3}}{2}$

D. $β = 60^{0}$

Câu 15:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB,

α

là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Tính sin

α

A. $\frac{\sqrt{17}}{17}$

B. $\frac{1}{\sqrt{34}}$

C. $\frac{2}{\sqrt{17}}$

D. $\frac{2}{\sqrt{34}}$

Góc giữa đường thẳng và mặt phẳng trong không gian

Giới thiệu

Liên kết

Chính sách

Kết nối

Góc giữa đường thẳng và mặt phẳng trong không gian

CHỌN BỘ SÁCH BẠN MUỐN XEM