Hàm số bậc hai

Câu 1:

Xác định Parabol (P):

y = a x^{2} + b x + 2

biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).

A. $y = - 5 x^{2} + 8 x + 2$

B. $y = 10 x^{2} + 13 x + 2$

C. $y = - 10 x^{2} - 13 x + 2$

D. $y = 9 x^{2} + 6 x - 5$

Câu 2:

Xác định Parabol (P):

y = a x^{2} + b x + 3

biết rằng Parabol có đỉnh I(3;−2).

A. $y = x^{2} - 6 x + 3$

B. $y = - \frac{5}{9} x^{2} + \frac{10}{3} x + 3$

C. $y = 3 x^{2} + 9 x + 3$

D. $y = \frac{5}{9} x^{2} - \frac{10}{3} x + 3$

Câu 3:

Xác định Parabol (P):

y = a x^{2} + b x - 5

biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −

\frac{3}{2}

A. $y = \frac{1}{18} x^{2} + \frac{1}{6} x - 5$

B. $y = \frac{1}{18} x^{2} + \frac{1}{6} x + 5$

C. $y = 3 x^{2} + 9 x - 9$

D. $y = - \frac{1}{18} x^{2} + \frac{1}{6} x - 5$

Câu 4:

Tìm các giá trị của tham số m để phương trình

2 x^{2} - 2 x + 1 - m = 0

có hai nghiệm phân biệt

A. $m > \frac{1}{2}$

B. $m = \frac{1}{2}$

C. $m < \frac{1}{2}$

D. Không tồn tại

Câu 5:

Cho hàm số

f (x) = x^{2} + 2 x - 3

Xét các mệnh đề sau:

(i)

f (x - 1) = x^{2} - 4

(ii) Hàm số đã cho đồng biến trên

(- 1; + \infty)

(iii) Giá trị nhỏ nhất của hàm số là một số âm.

(iv) Phương trình

f (x) = m

có nghiệm khi

m \geq - 4

Số mệnh đề đúng là:

A. 1

B. 2

C. 3

D. 4

Câu 6:

Tìm các giá trị của m để hàm số $y = x^{2} + m x + 5$ luôn đồng biến trên $(1; + \infty)$

A. m < −2

B. m ≥ −2

C. m = −4

D. Không xác định được

Câu 7:

Tìm giá trị của m để hàm số $y = - x^{2} + 2 x + m - 5$ đạt giá trị lớn nhất bằng 6

A. m = 0

B. m = 10

C. m = −10

D. Không xác định được

Câu 8:

Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2), B(−2;5), C(3;8)

A. $y = \frac{7}{10} x^{2} + \frac{1}{10} x - 2$

B. $y = \frac{7}{10} x^{2} - \frac{1}{10} x + 2$

C. $y = \frac{7}{10} x^{2} - \frac{1}{10} x - 2$

D. $y = \frac{7}{10} x^{2} + \frac{1}{10} x + 2$

Câu 9:

Cho phương trình của (P): $y = a x^{2} + b x + c (a \neq 0)$ biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A(2;0), B(−2;−8) Tính tổng $a^{2} + b^{2} + c^{2}$

A. $a^{2} + b^{2} + c^{2} = 3$

B. $a^{2} + b^{2} + c^{2} = \frac{29}{16}$

C. $a^{2} + b^{2} + c^{2} = \frac{48}{29}$

D. $[\begin{matrix} a^{2} + b^{2} + c^{2} = 5 \\ a^{2} + b^{2} + c^{2} = \frac{209}{16} \end{matrix}$

Câu 10:

Biết đồ thị hàm số (P): $y = x^{2} - (m^{2} + 1) x - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ x₁,x₂. Tìm giá trị của tham số mm để biểu thức $T = x_{1} + x_{2}$ đạt giá trị nhỏ nhất.

A. m > 0

B. m < 0

C. m = 0

D. Không xác định được

Câu 11:

Tìm các giá trị của tham số mm để phương trình $x^{2} - 2 (m + 1) x + 1 = 0$ có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).

A. m > 0

B. m < 0

C. m = 0

D. Không xác định được

Câu 12:

Tìm các giá trị của tham số m để

2 x^{2} - 2 (m + 1) x + m^{2} - 2 m + 4 \geq 0 (\forall x)

A. M = 3

B. $3 - \sqrt{2} < m < 3 + \sqrt{2}$

C. $[\begin{matrix} m \geq 3 + \sqrt{2} \\ m \leq 3 - \sqrt{2} \end{matrix}$

D. Không tồn tại

Câu 13:

Tìm giá trị nhỏ nhất của hàm số f(x) biết rằng $f (x + 2) = x^{2} - 3 x + 2$ trên $ℝ$

A. $- \frac{1}{4}$

B. $\frac{1}{4}$

C. $\frac{1}{2}$

D. 0

Câu 14:

Tìm giá trị của m để đồ thị hàm số $y = x^{2} - 2 x + m - 1$ cắt trục hoành tại hai điểm phân biệt có hoành độ dương.

A. $[\begin{matrix} m = 1 \\ m = 2 \end{matrix}$

B. $[\begin{matrix} m < 1 \\ m > 2 \end{matrix}$

C. 1 < m < 2

D. Không xác định được

Câu 15:

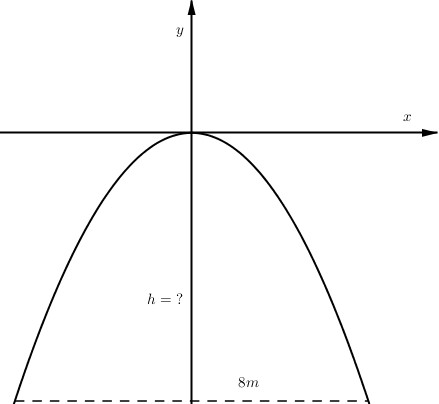
Tìm điểm A cố định mà họ đồ thị hàm số $y = x^{2} + (2 - m) x + 3 m (P_{m})$ luôn đi qua.

A.A(3;15)

B.A(0;−2)

C.A(3;−15)

D.A(−3;−15)

Câu 16:

Một chiếc cổng parabol dạng

y = - 12 x^{2}

có chiều rộng d = 8m. Hãy tính chiều cao h của cổng ?

Một chiếc cổng parabol dạng y=-12x^2 có chiều rộng d = 8m. Hãy tính (ảnh 1)

A. h = 8m.

B. h = 7m.

C. h = 9m.

D. h = 5m.

Câu 17:

Tìm các giá trị thực của tham số m để phương trình $|x^{2} - 3 x + 2| = m$ có bốn nghiệm thực phân biệt.

A. $m \geq \frac{1}{4}$

B. $0 < m < \frac{1}{4}$

C. m = 0

D. Không tồn tại

Câu 18:

Tìm các giá trị của tham số m để phương trình $\frac{1}{2} x^{2} - 4 |x| + 3 = m^{2}$ có 3 nghiệm thực phân biệt.

A.m = 3

B. $- \sqrt{3} < m < \sqrt{3}$

C. $m = \pm \sqrt{3}$

D. Không tồn tại

Câu 19:

Tìm các giá trị của m để phương trình $x^{2} - 2 x + \sqrt{4 x^{2} - 12 x + 9} = m$ có nghiệm duy nhất.

A. $- \frac{3}{4} < m < 0$

B. $- \frac{\sqrt{3}}{2} < m < \frac{\sqrt{3}}{2}$

C. $m = - \frac{3}{4}$

D. Không tồn tại

Câu 20:

Tìm giá trị nhỏ nhất của biểu thức

P = 3 (\frac{a^{2}}{b^{2}} + \frac{b^{2}}{a^{2}}) - 8 (\frac{a}{b} + \frac{b}{a})

A. $- \frac{34}{3}$

B.4

C.22

D.−10

Câu 21:

Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol (P). Biết rằng đạn của máy bắn đá bắn xa 100m và tại thời điểm đạn cao 60m thì đạn cách điểm bắn 80m.

Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol (P). Biết rằng đạn (ảnh 1)

Vị trí đạn bay cao nhất cách mặt đất bao nhiêu?

A.95,75m

B.96,75m

C.91,75m

D.93,75m

Câu 22:

Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol (P). Biết rằng đạn của máy bắn đá bắn xa 100m và tại thời điểm đạn cao 60m thì đạn cách điểm bắn 80m.

Máy bắn đá cách tường thành địch 90m. Biết tường thành cao 30m. Hỏi chiều cao khi đạn bay đến tường thành thì cao hơn hay thấp hơn tường thành bao nhiêu mét?

A.3,75m

B.33,75m

C.31,75m

D.1,75m

Câu 23:

Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol (P). Biết rằng đạn của máy bắn đá bắn xa 100m và tại thời điểm đạn cao 60m thì đạn cách điểm bắn 80m.

Đạn bắn ra từ 1 máy bắn đá có quỹ đạo là một parabol (P). Biết rằng đạn của (ảnh 1)

Địch xây chòi phòng thủ cao 20m phía trước tường thành. Hỏi phải đặt máy bắn đá cách chòi bao xa để đạn có thể bắn trúng chòi? Biết rằng để tránh bị địch tấn công thì máy bắn đá phải đặt cách thành địch ít nhất 50m.

A.93,35 m

B.95,35 m

C.94,35 m

D.95,85 m

Câu 24:

Bảng giá cước của một hãng taxi X được cho như bảng dưới đây:

Quãng đường	Giá cước (VNĐ/km)
Từ 0 đến 10 km	10 000
Từ trên 10 km đến 40 km	15 000
Trên 40 km	12 500

Thiết lập công thức liên hệ giữa quãng đường di chuyển và số tiền tương ứng phải trả. Nếu một người đi taxi của hãng X phải trả số tiền xe là 475000VNĐ thì người đó đã đi quãng đường là bao nhiêu?

A.35 km

B.36 km

C.37 km

D.38 km

Câu 25:

Bảng giá cước của một hãng taxi X được cho như bảng dưới đây:

Quãng đường	Giá cước (VNĐ/km)
Từ 0 đến 10 km	10 000
Từ trên 10 km đến 40 km	15 000
Trên 40 km	12 500

Một người đi taxi của hãng X từ A đến B, sau đó phải bắt taxi một lần nữa để đi từ B đến C. Biết quãng đường AB trong khoảng từ 10 đến 40 km, quãng đường BC dài hơn quãng đường AB là 32 km. Số tiền người đó phải trả ở quãng đường BC gấp 2,8 lần số tiền phải trả ở quãng đường AB. Tính độ dài quãng đường AB.

A.19 km

B.20 km

C.21 km

D.22 km

Câu 26:

Bảng giá cước của một hãng taxi X được cho như bảng dưới đây:

Quãng đường	Giá cước (VNĐ/km)
Từ 0 đến 10 km	10 000
Từ trên 10 km đến 40 km	15 000
Trên 40 km	12 500

Ngày Valentine, hãng X áp dụng chương trình giảm giá 10% cho khách hàng, tối đa 50000VNĐ. Một người đi taxi của hãng X trong dịp này phải trả 360000VNĐ thì người đó đã đi quãng đường là bao nhiêu?

A.10 km

B.15 km

C.25 km

D.30 km

Hàm số bậc hai

Giới thiệu

Liên kết

Chính sách

Kết nối

Hàm số bậc hai

CHỌN BỘ SÁCH BẠN MUỐN XEM