Sử dụng trường hợp bằng nhau của hai tam giác vuông để chứng minh tính chất khác
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
Cho ∆ABC vuông tại A và ∆MNP vuông tại M có AB = MN, CB = PN. Biết AC = 5 cm. Tính độ dài MP.
A. 4 cm;
B. 5 cm;
C. 6 cm;
D. 7 cm.
A. ∆AHB = ∆AHC theo trường hợp cạnh huyền – góc nhọn;
B. AH là phân giác \[\widehat {BAC}\];
C. BH = CH;
D. \[\widehat {ABH} = \widehat {ACH}\].
Cho ∆ABC có AI, BH, CK là các đường cao (I ∈ BC, K ∈ AB, H ∈ AC). Biết ∆ABH = ∆ACK. Kết luận nào sau đây đúng?
A. \[\widehat {HBA} \ne \widehat {KCA}\];
B. HB ≠ KC;
C. \[\widehat {ABH} = \widehat {KAC}\];
D. CH = BK.
Cho ∆ABC vuông tại A. Trên cạnh BC, lấy điểm D sao cho BD = BA = 5 cm. Đường thẳng vuông góc với BC tại D cắt AC tại H. Gọi E là giao điểm của DH và AB. Biết CD = 3 cm. Độ dài cạnh BE bằng
A. 3 cm;
B. 5 cm;
C. 8 cm;
D. 10 cm.
Tìm x trong hình bên.
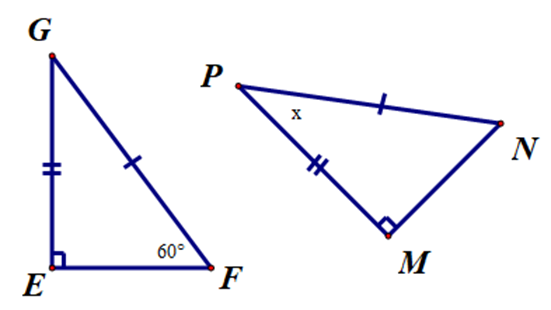
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Cho ∆ABC nhọn và ∆ABC = ∆DEF. Kẻ AH ⊥ BC (H ∈ BC) và DK ⊥ EF (K ∈ EF). Kết luận nào sau đây là đúng?
A. AH = DK;
B. BH = EK;
C. \[\widehat {BAH} = \widehat {EDK}\];
D. Cả A, B, C đều đúng.
Cho ∆ABC vuông tại A, tia phân giác \[\widehat B\] cắt AC tại D. Kẻ DE ⊥ BC tại E. Gọi H là giao điểm của BD và AE. Đường thẳng BH vuông góc với đường thẳng nào trong các đường thẳng sau đây.
A. AD;
B. AE;
C. AB;
D. Không có đường thẳng nào vuông góc với BH.
Cho hình vẽ:
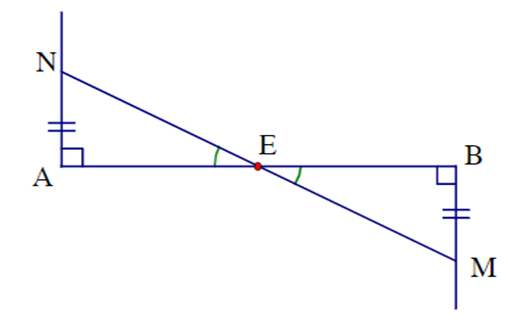
Kết luận nào sau đây sai?
A. E là trung điểm MN;
B. E là trung điểm AB;
C. \[\widehat {ANE} = \widehat {BME}\];
D. AE = ME.
Cho ∆ABC có M là trung điểm BC. Kẻ BE và CF lần lượt cùng vuông góc với AM ở E và F. Khi đó ta có BF song song với đường thẳng nào trong các đường thẳng sau đây.
A. CE;
B. MC;
C. AC;
D. AE.
Cho ∆ABC vuông tại A có AB < AC, \[\widehat B = 60^\circ \]. Kẻ AH ⊥ BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Kẻ DE ⊥ BC (E ∈ BC) và DK ⊥ AH (K ∈ AH). Cho các khẳng định sau:
(I) BH = AK;
(II) HA = KD = HE.
Chọn phương án đúng:
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I), (II) đều đúng;
D. Cả (I), (II) đều sai.
Các bài liên quan
Kiến thức bổ ích có thể giúp đỡ bạn rất nhiều:
