Thể tích khối hộp

Câu 1:

Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là:

A. $V = \frac{1}{3} S h$

B. $V = \frac{1}{2} S h$

C. $V = \frac{1}{6} S h$

D. $V = S h$

Câu 2:

Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích V. Trên đáy A′B′C′ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:

A. $\frac{V}{2}$

B. $\frac{2 V}{3}$

C. $\frac{V}{3}$

D. $\frac{3 V}{4}$

Câu 3:

Mệnh đề nào dưới đây sai?

A.Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau

B.Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau

C.Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau

D.Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau

Câu 4:

Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là tứ giác đều cạnh a, biết rằng $B D' = a \sqrt{6}$ . Tính thể tích của khối lăng trụ?

A. $a^{3} \sqrt{2}$

B. $a^{3} \sqrt{3}$

C. $3 a^{3}$

D. $2 a^{3}$

Câu 5:

Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ

A. $480 c m^{3}$

B. $360 c m^{3}$

C. $240 c m^{3}$

D. $120 c m^{3}$

Câu 6:

Cho lăng trụ xiên tam giác ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là $a \sqrt{3}$ và hợp với đáy ABC một góc 60⁰. Thể tích khối lăng trụ là:

A. $\frac{3 a^{3} \sqrt{3}}{8}$

B. $\frac{a^{3} \sqrt{3}}{8}$

C. $\frac{3 a^{3}}{8}$

D. $\frac{a^{3}}{8}$

Câu 7:

Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình thoi cạnh a và góc $\hat{A} = 60^{0}$ . Chân đường cao hạ từ B′ xuống (ABCD) trùng với giao điểm 2 đường chéo, biết $B B' = a$ . Thể tích khối lăng trụ là:

A. $\frac{3 a^{3}}{2}$

B. $\frac{3 a^{3}}{8}$

C. $\frac{3 a^{3}}{4}$

D. $\frac{a^{3}}{4}$

Câu 8:

Cho hình lăng trụ ABC.A′B′C′ có $A B = 2 a, A C = a, A A' = \frac{a \sqrt{10}}{2}, \hat{B A C} = 120^{0}$ . Hình chiếu vuông góc của C′ lên (ABC) là trung điểm của cạnh BC. Tính thể tích khối lăng trụ ABC.A′B′C′ theo a?

A. $\frac{a^{3} \sqrt{3}}{4}$

B. $\frac{3 a^{3}}{4}$

C. $\frac{3 a^{3} \sqrt{3}}{4}$

D. $a^{3} \sqrt{3}$

Câu 9:

Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A′ trên mặt phẳng (ABCD) là trung điểm I của cạnh AB. Biết A′C tạo với mặt phẳng đáy một góc $α$ với $t a n α = \frac{2}{\sqrt{5}}$ . Thể tích khối chóp A′.ICD là:

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3} \sqrt{3}}{6}$

C. $\frac{a^{3} \sqrt{3}}{3}$

D. $\frac{a^{3}}{3}$

Câu 10:

Cho khối lăng trụ tam giác ABC.A′B′C′ mà mặt bên ABB′A′ có diện tích bằng 4. Khoảng cách giữa CC′ và mặt phẳng $(A B B' A')$ bằng 7. Thể tích khối lăng trụ là:

A.10

B.12

C.14

D.16

Câu 11:

Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông tại $B, \hat{A C B} = 60^{0}$ , cạnh BC=a, đường chéo A′B tạo với mặt phẳng (ABC) một góc 30⁰. Thể tích khối lăng trụ ABC.A′B′C′ là:

A. $\frac{a^{3} \sqrt{3}}{2}$

B. $\frac{a^{3} \sqrt{3}}{3}$

C. $a^{3} \sqrt{3}$

D. $\frac{3 a^{3} \sqrt{3}}{2}$

Câu 12:

Đáy của hình lăng trụ đứng tam giác ABC.A′B′C′ là tam giác đều cạnh $a = 4$ và biết diện tích tam giác A′BC bằng 8 . Tính thể tích khối lăng trụ?

A.8

B. $8 \sqrt{3}$

C. $\frac{8 \sqrt{3}}{3}$

D. $16 \sqrt{3}$

Câu 13:

Cho lăng trụ đều ABC.A′B′C′, cạnh đáy bằng a, góc giữa hai mặt phẳng $(A' B C)$ và (ABC) bằng 60⁰. Tính thể tích khối lăng trụ đó.

A. $\frac{a^{3} \sqrt{3}}{8}$

B. $\frac{3 a^{3} \sqrt{3}}{4}$

C. $\frac{3 a^{3} \sqrt{3}}{8}$

D. $\frac{a^{3} \sqrt{3}}{4}$

Câu 14:

Cho khối lăng trụ ABC.A′B′C′. Gọi E là trọng tâm tam giác A′B′C′ và F là trung điểm BC. Gọi

V_{1}

là thể tích khối chóp B′.EAF và

V_{2}

là thể tích khối lăng trụ ABC.A′B′C′. Khi đó

\frac{V_{1}}{V_{2}}

có giá trị bằng

A. $\frac{1}{5}$

B. $\frac{1}{4}$

C. $\frac{1}{6}$

D. $\frac{1}{8}$

Câu 15:

Cho lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, và $A' A = A' B = A' C = a \sqrt{\frac{7}{12}}$ . Thể tích khối lăng trụ ABC.A′B′C′ theo a là:

A. $\frac{a^{3}}{8}$

B. $\frac{a^{3} \sqrt{3}}{8}$

C. $\frac{3 a^{3} \sqrt{3}}{8}$

D. $\frac{a^{3} \sqrt{3}}{4}$

Câu 16:

Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác cân $A B = A C = a; \hat{B A C} = 120^{0}$ và AB′ vuông góc với $(A' B' C')$ . Mặt phẳng $(A A' C')$ tạo với mặt phẳng $(A' B' C')$ một góc 30⁰. Thể tích khối lăng trụ ABC.A′B′C′ là:

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $\frac{8 a^{3}}{3}$

C. $\frac{a^{3} \sqrt{3}}{8}$

D. $\frac{a^{3} \sqrt{3}}{2}$

Câu 17:

Cho hình lăng trụ ABC.A′B′C′ có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C trên (ABB′A′) là tâm của hình bình hành ABB′A′. Thể tích của khối lăng trụ là:

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3} \sqrt{2}}{2}$

C. $\frac{a^{3} \sqrt{2}}{4}$

D. $\frac{a^{3}}{2}$

Câu 18:

Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình chữ nhật với $A B = \sqrt{3}, A D = \sqrt{7}$ . Hai mặt bên $(A B B' A')$ và $(A D D' A')$ lần lượt tạo với đáy những góc 45⁰ và 60⁰. Tính thể tích khối hộp nếu biết cạnh bên bằng 1.

A. $V = 3$

B. $V = 2$

C. $V = 4$

D. $V = 8$

Câu 19:

Cho hình lăng trụ xiên ABC.A′B′C′ có đáy ABC là tam giác đều với tâm O. Hình chiếu của C′ trên (ABC) là O. Tính thể tích của lăng trụ biết rằng khoảng cách từ O đến CC′ là a và 2 mặt bên (ACC′A′) và (BCC′B′) hợp với nhau góc 90⁰.

A. $\frac{a^{3} \sqrt{2}}{4}$

B. $\frac{3 a^{3} \sqrt{2}}{8}$

C. $\frac{9 a^{3} \sqrt{2}}{8}$

D. $\frac{27 a^{3} \sqrt{2}}{8}$

Câu 20:

Cho lăng trụ đứng ABC.A′B′C′ với ABC là tam giác vuông cân tại C có $A B = a$ , mặt bên ABB′A′ là hình vuông. Mặt phẳng qua trung điểm I của AB và vuông góc với AB′ chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?

A. $V_{1} = \frac{a^{3}}{48}, V_{2} = \frac{11 a^{3}}{24}$

B. $V_{1} = \frac{a^{3}}{24}, V_{2} = \frac{11 a^{3}}{48}$

C. $V_{1} = \frac{a^{3}}{48}, V_{2} = \frac{11 a^{3}}{48}$

D. $V_{1} = \frac{a^{3}}{24}, V_{2} = \frac{5 a^{3}}{24}$

Câu 21:

Cho đa diện ABCDEF có AD,BE,CF đôi một song song. $A D ⊥ (A B C), A D + B E + C F = 5$ , diện tích tam giác ABC bằng 10. Thể tích đa diện ABCDEF bằng

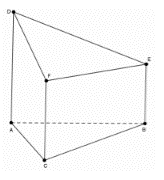
Media VietJack

A.50

B. $\frac{15}{2}$

C. $\frac{50}{3}$

D. $\frac{15}{4}$

Câu 22:

Cho hình hộp $A B C D . A' B' C' D'$ có thể tích bằng V. Gọi M,N,P,Q,E,F lần lượt là tâm các hình bình hành $A B C D, A' B' C' D', A B B' A', B C C' B', C D D' C', D A A' D'$ . Thể tích khối đa diện có các đỉnh M,P,Q,E,F,N bằng:

A. $\frac{V}{4}$

B. $\frac{V}{2}$

C. $\frac{V}{6}$

D. $\frac{V}{3}$

Câu 23:

Cho hình lăng trụ tam giác đều ABC.A′B′C′có $A B = a$ , đường thẳng A′B tạo với mặt phẳng $(B C C' B')$ một góc 30⁰. Tính thể tích khối lăng trụ ABC.A′B′C′.

A. $\frac{3 a^{3}}{2}$

B. $\frac{a^{3} \sqrt{6}}{4}$

C. $\frac{3 a^{3}}{4}$

D. $\frac{a^{3} \sqrt{3}}{4}$

Câu 24:

Cho hình lăng trụ tam giác ABC.A′B′C′ có diện tích đáy bằng 12 và chiều cao bằng 6. Gọi M,N lần lượt là trung điểm của CB,CA và P,Q,R lần lượt là tâm các hình bình hành ABB′A′, BCC′B′, CAA′C′. Thể tích của khối đa diện PQRABMN bằng:

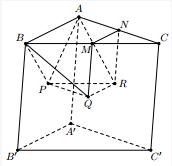
Media VietJack

A.42

B.14

C.18

D.21

Câu 25:

Cho hình hộp chữ nhật ABCD⋅A′B′C′D′ có M,N,P lần lượt là trung điểm các cạnh BC,C′D′,DD′ (tham khảo hình vẽ). Biết thể tích khối hộp bằng 144 , thể tích khối tứ diện AMNP bằng

A. 15

B. 18

C. 20

D. 24

Câu 26:

Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác vuông tại A. Cạnh $B C = 2 a$ và $∠ A B C = 60^{0}$ . Biết tứ giác BCC′B′ là hình thoi có $∠ B' B C$ nhọn. Mặt phẳng $(B C C' B')$ vuông góc với (ABC) và mặt phẳng $(A B B' A')$ tạo với (ABC) góc 45⁰. Thể tích khối lăng trụ ABC.A′B′C′ bằng:

A. $\frac{\sqrt{7} a^{3}}{7}$

B. $\frac{3 \sqrt{7} a^{3}}{7}$

C. $\frac{6 \sqrt{7} a^{3}}{7}$

D. $\frac{\sqrt{7} a^{3}}{21}$

Câu 27:

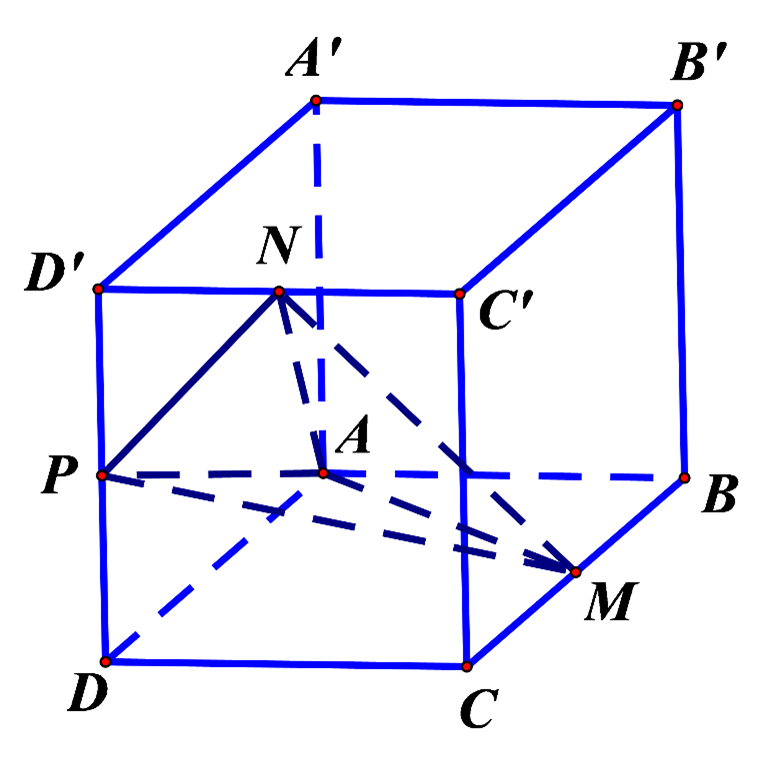
Cho hình lập phương ABCD.A′B′C′D′ có thể tích V. Gọi M là điểm thuộc cạnh BB′ sao cho $M B = 2 M B' .$ Mặt phẳng $(α)$ đi qua M và vuông góc với AC′ cắt các cạnh DD′, DC, BC lần lượt tại N, P, Q. Gọi $V_{1}$ là thể tích của khối đa diện CPQMNC′.Tính tỉ số $\frac{V_{1}}{V}$

A. $\frac{31}{162}$

B. $\frac{35}{162}$

C. $\frac{34}{162}$

D, $\frac{13}{162}$

Câu 28:

Đề thi THPT QG - 2021 - mã 101

Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, $B D = 2 a$ , góc giữa hai mặt phẳng (A′BD) và (ABCD) bằng 30⁰. Thể tích của khối hộp chữ nhật đã cho bằng

A. $6 \sqrt{3} a^{3} .$

B. $\frac{2 \sqrt{3}}{9} a^{3} .$

C. $2 \sqrt{3} a^{3} .$

D. $\frac{2 \sqrt{3}}{3} a^{3} .$

Câu 29:

Cho hình lập phương ABCD.A′B′C′D′ cạnh 2a, gọi M là trung điểm của BB′ và P thuộc cạnh DD′ sao cho $D P = \frac{1}{4} D D' .$ Mặt phẳng (AMP) cắt CC′ tại N. Thể tích khối đa diện AMNPBCD bằng

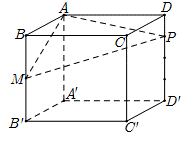
Media VietJack

A. $V = 2 a^{3} .$

B. $V = 3 a^{3} .$

C. $V = \frac{11 a^{3}}{3} .$

D. $V = \frac{9 a^{3}}{4} .$

Câu 30:

Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông,

A B = B C = a .

. Biết rằng góc giữa hai mặt phẳng (ACC′) và (AB′C′) bằng 60⁰ (tham khảo hình vẽ bên). Thể tích của khối chóp B′.ACC′A′ bằng

A. $\frac{a^{3}}{3} .$

B. $\frac{a^{3}}{6} .$

C. $\frac{a^{3}}{2} .$

D. $\frac{\sqrt{3} a^{3}}{3} .$

Câu 31:

Cho hình hộp ABCD.A′B′C′D′. Gọi E,F lần lượt là trung điểm của B′C′ và C′D′. Mặt phẳng (AEF) chia hình hộp thành hai hình đa diện (H) và (H′) trong đó (H) là hình đa diện chứa đỉnh A′. Tính tỉ số thể tích đa diện (H) và thể tích hình đa diện (H′).

A. $\frac{25}{47}$

B. $\frac{25}{72}$

C. $\frac{47}{25}$

D. $\frac{72}{47}$

Câu 32:

Cho lăng trụ tam giác ABC.A′B′C′ có đáy ABC là đều cạnh

A B = 2 a \sqrt{2}

. Biết

A C' = 8 a

và tạo với mặt đáy một góc 45⁰. Thể tích khối đa diện ABCC′B′ bằng

A. $\frac{8 a^{3} \sqrt{3}}{3} .$

B. $\frac{8 a^{3} \sqrt{6}}{3} .$

C. $\frac{16 a^{3} \sqrt{3}}{3} .$

D. $\frac{16 a^{3} \sqrt{6}}{3} .$

Câu 33:

Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H₁, H₂ lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của $\frac{V_{(H_{1})}}{V_{(H_{2})}}$ bằng

A.4

B.2

C.5

D.3

Câu 34:

Tính góc giữa hai mặt phẳng (ABB′A′) và (ABC)

A. $30^{0}$

B. $45^{0}$

C. $60^{0}$

D. $90^{0}$

Thể tích khối hộp

Giới thiệu

Liên kết

Chính sách

Kết nối

Thể tích khối hộp

CHỌN BỘ SÁCH BẠN MUỐN XEM