Tính số đo các góc dựa vào tính chất góc ở vị trí đặc biệt, định nghĩa tia phân giác

  • 1Làm xong biết đáp án, phương pháp giải chi tiết.
  • 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
  • 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
  • 4Biết điểm yếu và có hướng giải pháp cải thiện

Số câu đúng

0/10

Thời gian làm bài

00:00:00

Số câu đã làm

0

Câu 1:

Cho hình vẽ sau. Số đo \(\widehat {xOx'}\) là:

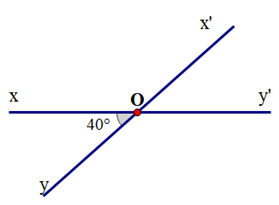
Media VietJack

A. 40°;
B. 50°;
C. 140°;
D. 130°.
Câu 2:

Cho hình vẽ sau. Số đo \(\widehat {{\rm{x'Oy}}'}\) là:

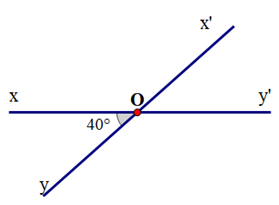
Media VietJack

A. 40°;
B. 50°;
C. 140°;
D. 130°.
Câu 3:

Cho \(\widehat {xOy} = {30^o}\); Oy là tia phân giác \(\widehat {xOz}\). Khi đó \(\widehat {xOz}\) bằng:

A. 90°;
B. 60°;
C. 15°;
D. 120°.
Câu 4:

Ot là tia phân giác của \(\widehat {xOy}\) khi:

A. Tia Ot nằm giữa hai tia Ox và Oy;
B. \(\widehat {xOt} = \widehat {tOy}\);
C. \(\widehat {xOt} = \widehat {yOt} = \frac{1}{2}\widehat {xOy}\);
D. \(\widehat {xOt} + \widehat {tOy} = \widehat {xOy}\).
Câu 5:
Tia phân giác của một góc là
A. tia tạo với hai cạnh của góc hai góc bằng nhau;
B. tia nằm giữa hai cạnh của một góc;
C. tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau;
D. tia trùng với một trong hai cạnh của góc.
Câu 6:

Cho \(\widehat {xOy}\)và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy}\) = 60° và tia Ot là tia phân giác của \(\widehat {yOz}\). Số đo góc \(\widehat {xOt}\) là:

A. 80°;
B. 30°;
C. 60°;
D. 120°.
Câu 7:

Cho hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho \(\widehat {xOy} = {60^o}\). Gọi Ot là tia phân giác của \(\widehat {x'Oy}'\). Số đo \(\widehat {xOt}\) là:

A. 150°;
B. 30°;
C. 90°;
D. 120°.
Câu 8:
Cho góc bẹt \(\widehat {aOb}\). Gọi Oc là tia phân giác của \(\widehat {aOb}\); Ox là phân giác của \(\widehat {aOc}\); Oy là phân giác của \(\widehat {cOb}\). Số đo \(\widehat {xOy}\) là:
A. 90°;
B. 45°;
C. 100°;
D. 135°.
Câu 9:

Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết \(\widehat {xOy'} - \widehat {xOy} = {90^o}\). Tính \(\widehat {xOy}\).

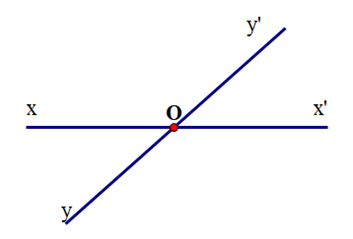
Media VietJack

A. 40°;
B. 45°;
C. 90°;
D. 135°.
Câu 10:

Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết \(\widehat {xOy'} = 2\widehat {xOy}\). Tính \(\widehat {xOy}\).

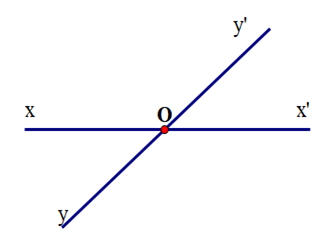
Media VietJack

A. 60°;
B. 30°;
C. 120°;
D. 90°.

Các bài liên quan

Kiến thức bổ ích có thể giúp đỡ bạn rất nhiều:

Leson Icon Lý thuyết Tính số đo các góc dựa vào tính chất góc ở vị trí đặc biệt, định nghĩa tia phân giác