Ứng dụng tích phân vào tính diện tích
- 1Làm xong biết đáp án, phương pháp giải chi tiết.
- 2Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
- 3Xem lại lý thuyết, lưu bài tập và note lại các chú ý
- 4Biết điểm yếu và có hướng giải pháp cải thiện
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
A. S=2+e
B. S=2-e
C. S=e-2
D. S=e-1
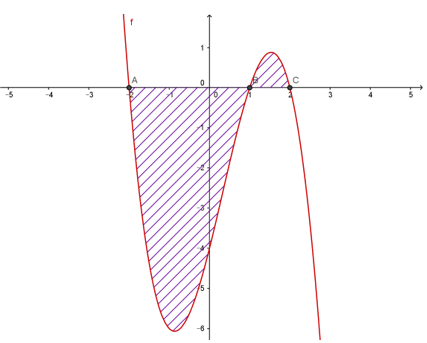
A.
B.
C.
D.
Cho hàm số f(x) có đồ thị trên đoạn [-3;3]là đường gấp khúc ABCD như hình vẽ.
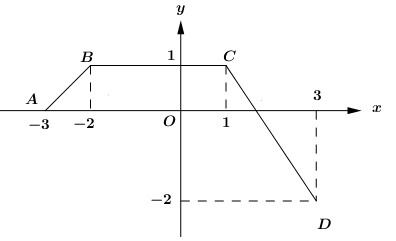
Tính
A.
B.
C.
D.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng x=1, x=2 bằng: (Đáp án là phân số tối giản)
A.
B.
C.
D.
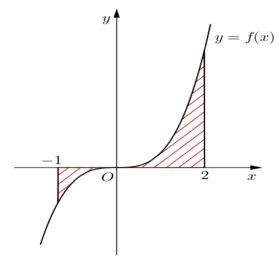
A. S=b-a
B. S=b+a
C. S=-b+a
D. S=-b-a
A.
B.
C.
D.
A.
B.
C.
D.
A. 0
B. 16
C. 4
D. 8
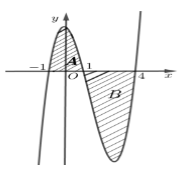
A.
B.
C.
D.
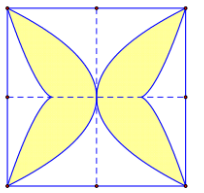
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).
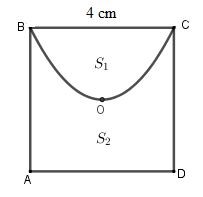
Tỉ số bằng:
A.
B.
C.
D.
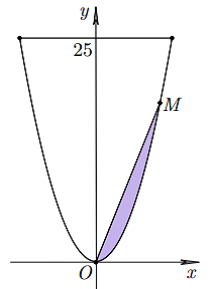
Cho parabol và đường thẳng (d);y=mx+2. Biết rằng tồn tại m để diện tích hình phẳng giới hạn bới(P) và (d) đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.
A.
B.
C. S = 4
D.
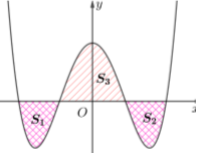
A. 3
B. -4
C. 6
D. -2
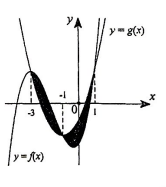
A.
B.
C. 4
D. 5
A. 2ln3
B. ln3
C. ln18
D. 2ln2
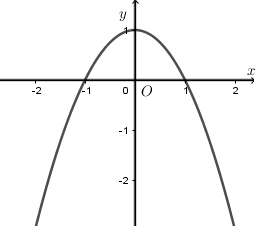
A.
B. S = 1
C.
D. S = 2
A.
B.
C.
D.
A.
B.
C.
D.
A.
B.
C.
D.
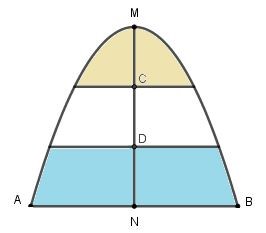
Một khung cửa kính hình parabol với đỉnh M và cạnh đáy AB như minh họa ở hình bên. Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200.000 đồng /m2 và phần kính trắng còn lại là 150.000 đồng /m2.Cho . Hỏi số tiền để lắp kính cho khung cửa như trên gần nhất với số tiền nào dưới đây?
A. 1.954.000 đồng
B. 2.123.000 đồng
C. 1.946.000 đồng
A. 30kg
B. 40kg
C. 50kg