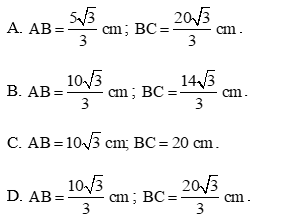Câu hỏi:
187 lượt xem Tự luận
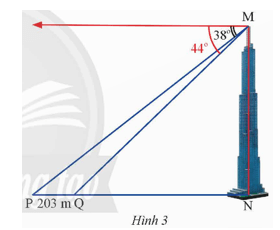
Hai điểm P và Q cách nhau 203 m và thẳng hàng với chân của một tòa tháp (Hình 3). Từ đỉnh của tòa tháp đó, một người nhìn thấy hai điểm P, Q với hai góc nghiêng xuống lần lượt là 38° và 44°. Tính chiều cao của tòa tháp (kết quả làm tròn đến hàng đơn vị của mét).
Lời giải
Hướng dẫn giải:
Ta có >; ;
• Xét tam giác MPN vuông tại N, ta có:
• Xét tam giác MQN vuông tại N, ta có:
Mặt khác, ta có PN – QN = PQ = 203
Suy ra
Vậy chiều cao của tòa tháp khoảng 831 m.
Câu 1:
Tự luận
Cho tam giác ABC vuông tại A có AC = 10 cm, Độ dài hai cạnh còn lại là
1 năm trước
85 lượt xem
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Tự luận
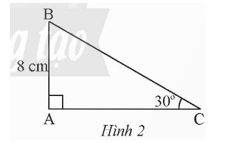
Cho tam giác OPQ vuông tại O có và PQ = 10 cm. Hãy giải tam giác vuông OPQ.
1 năm trước
83 lượt xem