Câu hỏi:
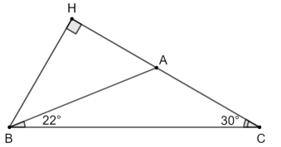
157 lượt xemCho tam giác ABC có BC = 20 cm,
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
b) Tính các cạnh và các góc còn lại của tam giác ABC.
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
Lời giải
Hướng dẫn giải:
a) Gọi BH là đường cao hạ từ B xuống AC.
Khi đó, BH là khoảng cách từ điểm B đến đường thẳng AC.
Xét tam giác BHC có , ta có:
BH = BC . sin 30° = 20 . sin 30° = 10 (cm).
Vậy khoảng cách từ điểm B đến đường thẳng AC là 10 cm.
b) Xét tam giác ABC, ta có: .
Suy ra
Ta có
Xét tam giác ABH vuông tại H có nên
• suy ra .
• suy ra .
Áp dụng định lý Pythagore vào tam giác BHC, ta có: BC2 = CH 2 + BH2
Suy ra .
Do đó .
Vậy độ dài các cạnh và các góc còn lại của tam giác ABC là , AB ≈ 7,9 cm, AC ≈ 9,5 cm.
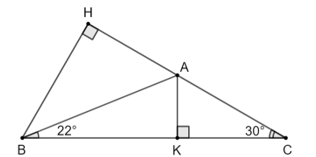
c) Gọi AK là đường cao hạ từ A xuống BC.
Khi đó, AK là khoảng cách từ điểm A đến đường thẳng BC.
Xét tam giác ACK có và AC ≈ 9,5 cm nên ta có:
Vậy khoảng cách từ điểm A đến đường thẳng BC khoảng 4,8 cm.
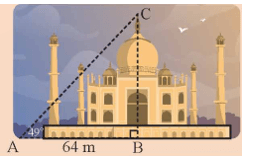
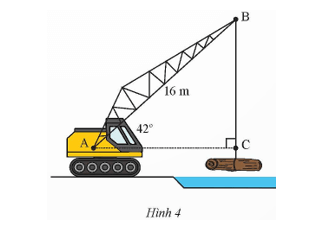
Làm thế nào để tính chiều cao BC khi biết khoảng cách AB và góc A trong hình bên?
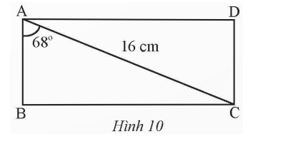
Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và (Hình 10).
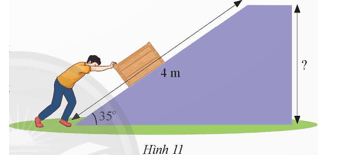
Một người đẩy một vật lên hết một con dốc nghiêng một góc 35° (Hình 11).
ĐỀ THI LIÊN QUAN:
-
11 câu hỏi 78 lượt thi -
16 câu hỏi 55 lượt thi