Câu hỏi:
168 lượt xem Tự luận
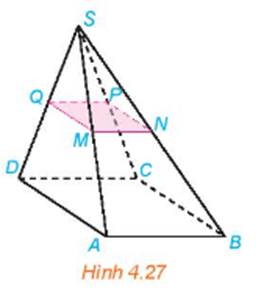
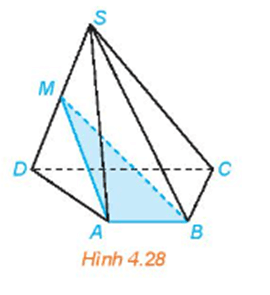
Bài 4.11 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành.
Lời giải
Hướng dẫn giải:
Xét tam giác SAB có M và N lần lượt là trung điểm của các cạnh SA và SB nên MN là đường trung bình của tam giác SAB, suy ra MN // AB và MN = AB.
Tương tự ta có PQ là đường trung bình của tam giác SCD nên PQ // CD và PQ = CD.
Lại có đáy ABCD là hình bình hành nên AB // CD và AB = CD.
Khi đó, MN // PQ và MN = PQ. Vậy tứ giác MNPQ là hình bình hành.
Câu 2:
Câu 3:
Câu 5:
Câu 6:
Câu 8:
Câu 9:
Câu 11:
Câu 12:
Câu 14:
Câu 16:
Câu 18: