Câu hỏi:
125 lượt xem Tự luận
Bài 4.17 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các vectơ và các điểm M(‒3;6), N(3;‒3).
a) Tìm mối liên hệ giữa các vectơ và
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x;y) để OMNP là hình bình hành.
Lời giải
Hướng dẫn giải:
Lời giải
a) Ta có:
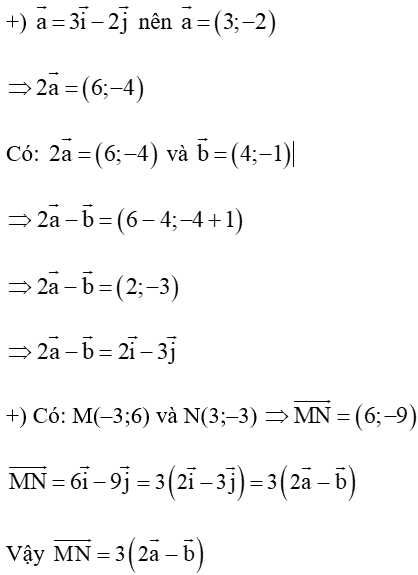
b) Ta có
+ M(-3; 6)
+) N(3;‒3)
Hai vectơ không cùng phương (vì ).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy ba điểm O, M, N không thẳng hàng.
c)
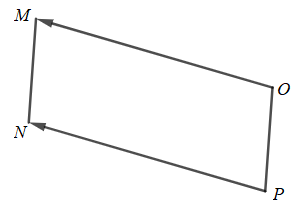
Các điểm O, M, N không thẳng hàng, tứ giác OMNP là hình bình hành khi và chỉ khi
Ta có: M(‒3;6); N(3;‒3) và P(x; y)
Do đó
Vậy điểm cần tìm là P(6;‒9).