Giải Toán 10 (Kết nối tri thức) Bài 10: Vectơ trong mặt phẳng tọa độ

Sinx.edu.vn xin giới thiệu giải bài tập Toán lớp 10 Bài 10: Vectơ trong mặt phẳng tọa độ sách Kết nối tri thức hay nhất, chi tiết giúp học sinh so sánh và làm bài tập Toán 10 dễ dàng. Mời các bạn đón xem:

1 195 lượt xem

Bài trước

Bài sau

Giải bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ

Mở đầu

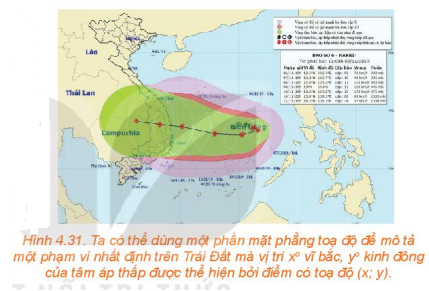
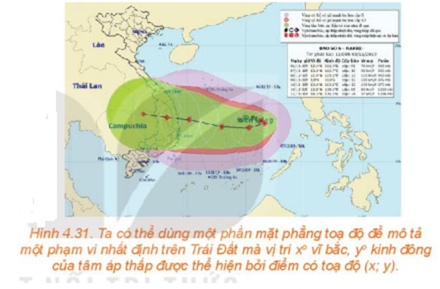
Mở đầu trang 60 Toán 10 Tập 1: Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?

Sau bài học này ta có thể trả lời câu hỏi trên như sau:

Gọi M(x; y) là vị trí của tâm bão tại thời điểm bất kì t giờ trong khoảng thời gian 12 giờ.

Do bão di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3) nên điểm M thuộc đoạn thẳng AB.

Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão (ảnh 1)

Theo dự báo, tại thời điểm t giờ thì tâm bão đã đi được một khoảng AM là: $\frac{A M}{A B} = \frac{t}{12}$

Hay $A M = \frac{t}{12} A B$

Vectơ $\vec{A M}$ cùng hướng với vectơ $\vec{A B}$ và $A M = \frac{t}{12} A B$ nên $\vec{A M} = \frac{t}{12} \vec{A B}$

Ta có: A(13,8; 108,3); B(14,1; 106,3); M(x; y)

Suy ra $\vec{A M} = (x - 13, 8; y - 108, 3), \vec{A B} = (0, 3; - 2)$

Ta có: $\vec{A M} = \frac{t}{12} \vec{A B}$ $\Leftrightarrow \{\begin{cases} x - 13, 8 = \frac{t}{12} .0, 3 \\ y - 108, 3 = \frac{t}{12} . (- 2) \end{cases} \Leftrightarrow \{\begin{cases} x = 0, 3. \frac{t}{12} + 13, 8 \\ y = - 2. \frac{t}{12} + 108, 3 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{t}{40} + 13, 8 \\ y = - \frac{t}{6} + 108, 3 \end{cases}$

$\Rightarrow M (\frac{t}{40} + 13, 8; - \frac{t}{6} + 108, 3)$

Vậy ở thời điểm t giờ tâm bão là điểm M ở vị trí $M (\frac{t}{40} + 13, 8; - \frac{t}{6} + 108, 3)$

1. Tọa độ của Vecto

Giải Toán 10 trang 60 Tập 1

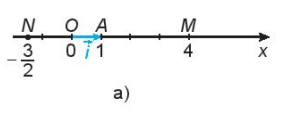
HĐ 1 trang 60 Toán 10 Tập 1: Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt $\vec{O A} = \vec{i}$ (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số $- \frac{3}{2} .$ Hãy biểu thị mỗi vectơ $\vec{O M}, \vec{O N}$ theo vectơ đơn vị $\vec{i} .$

Trên hình vẽ ta thấy:

+) Vectơ $\vec{O M}$ cùng hướng với vectơ $\vec{O A}$ và OM = 4 = 4.1 = 4OA

Nên $\vec{O M} = 4 \vec{O A} = 4 \vec{i}$ .

+) Vectơ $\vec{O N}$ ngược hướng với vectơ $\vec{O A}$ và ON = $\frac{3}{2} = \frac{3}{2} .1 = \frac{3}{2}$ OA

Nên $\vec{O N} = - \frac{3}{2} \vec{O A} = - \frac{3}{2} \vec{i}$ .

Vậy $\vec{O M} = 4 \vec{i}$ và $\vec{O N} = - \frac{3}{2} \vec{i}$ .

Giải Toán 10 trang 61 Tập 1

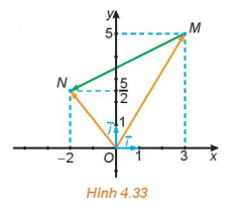
HĐ 2 trang 61 Toán 10 Tập 1: Trong Hình 4.33:

a) Hãy biểu thị mỗi vectơ $\vec{O M}, \vec{O N}$ theo các vectơ $\vec{i}, \vec{j}$ .

b) Hãy biểu thị vectơ $\vec{M N}$ theo các vectơ $\vec{O M}, \vec{O N}$ từ đó biểu thị vectơ $\vec{M N}$ theo các vectơ $\vec{i}, \vec{j}$ .

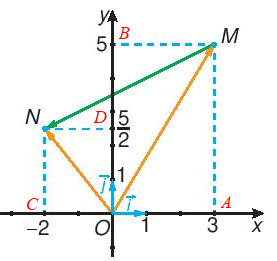
Trong Hình 4.33: Hãy biểu thị mỗi vectơ OM,ON theo các vecto i, j (ảnh 1)

Giả sử các điểm A, B, C, D được biểu diễn như hình vẽ trên.

Khi đó $\vec{O A} = 3 \vec{i}; \vec{O B} = 5 \vec{j}; \vec{O C} = - 2 \vec{i}; \vec{O D} = \frac{5}{2} \vec{j} .$

a) OAMB là hình bình hành suy ra $\vec{O M} = \vec{O A} + \vec{O B}$ (quy tắc hình bình hành)

Do đó $\vec{O M} = 3 \vec{i} + 5 \vec{j}$

OCND là hình bình hành suy ra $\vec{O N} = \vec{O C} + \vec{O D}$ (quy tắc hình bình hành)

Do đó $\vec{O N} = - 2 \vec{i} + \frac{5}{2} \vec{j}$

b) Ta có: $\vec{M N} = \vec{O N} - \vec{O M}$ (quy tắc ba điểm)

$\vec{M N} = (- 2 \vec{i} + \frac{5}{2} \vec{j}) - (3 \vec{i} + 5 \vec{j}) = - 2 \vec{i} + \frac{5}{2} \vec{j} - 3 \vec{i} - 5 \vec{j} = (- 2 \vec{i} - 3 \vec{i}) + (\frac{5}{2} \vec{j} - 5 \vec{j}) = - 5 \vec{i} - \frac{5}{2} \vec{j} .$

Vậy $\vec{M N} = \vec{O N} - \vec{O M} = - 5 \vec{i} - \frac{5}{2} \vec{j} .$

Luyện tập 1 trang 61 Toán 10 Tập 1: Tìm tọa độ của $\vec{0}$ .

Ta có: $\vec{0} = 0. \vec{i} + 0. \vec{j} \Rightarrow \vec{0} = (0; 0)$ .

Vậy vectơ $\vec{0}$ có toạ độ là (0; 0).

2. Biểu thức tọa độ của các phép toán vecto

HĐ 3 trang 61 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho $\vec{u} = (2; - 3), \vec{v} = (4; 1), \vec{a} = (8; - 12) .$

a) Hãy biểu thị mỗi vectơ $\vec{u}, \vec{v}, \vec{a}$ theo các vectơ $\vec{i}, \vec{j} .$

b) Tìm tọa độ của các vectơ $\vec{u} + \vec{v}, 4 \vec{u} .$

c) Tìm mối liên hệ giữa hai vectơ $\vec{u}, \vec{a} .$

a) Ta có:

$\vec{u} = (2; - 3) \Rightarrow \vec{u} = 2 \vec{i} - 3 \vec{j};$

$\vec{v} = (4; 1) \Rightarrow \vec{v} = 4 \vec{i} + \vec{j};$

$\vec{a} = (8; - 12) \Rightarrow \vec{a} = 8 \vec{i} - 12 \vec{j} .$

b) Ta có:

$\vec{u} + \vec{v} = (2 \vec{i} - 3 \vec{j}) + (4 \vec{i} + \vec{j}) = 2 \vec{i} - 3 \vec{j} + 4 \vec{i} + \vec{j} = 6 \vec{i} - 2 \vec{j} \Rightarrow \vec{u} + \vec{v} = (6; - 2)$

$4 \vec{u} = 4 (2 \vec{i} - 3 \vec{j}) = 8 \vec{i} - 12 \vec{j} \Rightarrow 4 \vec{u} = (8; - 12) .$

Vậy toạ độ của vectơ $\vec{u} + \vec{v}$ là (6; ‒2) và toạ độ của vectơ $4 \vec{u}$ là (8; ‒12).

c) Ta có $\vec{a} = (8; - 12)$ và $4 \vec{u} = (8; - 12) .$

Suy ra $\vec{a} = 4 \vec{u}$ .

Vậy $\vec{a} = 4 \vec{u}$ .

Giải Toán 10 trang 62 Tập 1

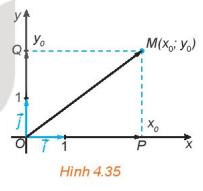
HĐ 4 trang 62 Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy, cho điểm M(x0;y0).

Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).

a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị $\vec{O P}$ theo $\vec{i}$ và tính độ dài của $\vec{O P}$ theo x0.

b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị $\vec{O Q}$ theo $\vec{j}$ và tính độ dài của $\vec{O Q}$ theo y0.

c) Dựa vào hình chữ nhật OPMQ, tính độ dài của $\vec{O M}$ theo x0, y0.

d) Biểu thị $\vec{O M}$ theo các vectơ $\vec{i}, \vec{j}$ .

a) Trên trục Ox, điểm P biểu diễn cho số x0 nên OP = |x0| = x0.

Ta có vectơ $\vec{O P}$ cùng hướng với vectơ $\vec{i}$ và $|\vec{O P}| =$ OP = x0 nên $\vec{O P} = x_{0} \vec{i} .$

Vậy $\vec{O P} = x_{0} \vec{i} .$

b) Trên trục Oy, điểm Q biểu diễn cho số y0 nên OQ = |y0| = y0.

Ta có vectơ $\vec{O Q}$ cùng hướng với vectơ $\vec{j}$ và $|\vec{O Q}| =$ OQ = y0 nên $\vec{O Q} = y_{0} \vec{j} .$

Vậy $\vec{O Q} = y_{0} \vec{j} .$

c) Xét tam giác OPM vuông tại P, theo định lí Pythagore ta có: OM2 = OP2 + MP2

$\Rightarrow O M = \sqrt{O P^{2} + M P^{2}} = \sqrt{O P^{2} + O Q^{2}} = \sqrt{x_{0}^{2} + y_{0}^{2}} .$

Do đó $|\vec{O M}| = O M = \sqrt{x_{0}^{2} + y_{0}^{2}} .$

Vậy $|\vec{O M}| = \sqrt{x_{0}^{2} + y_{0}^{2}} .$

d) Ta có $\vec{O M} = \vec{O P} + \vec{O Q} = x_{0} \vec{i} + y_{0} \vec{j}$ .

Vậy $\vec{O M} = x_{0} \vec{i} + y_{0} \vec{j} .$

HĐ 5 trang 62 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x'; y').

a) Tìm tọa độ của các vectơ $\vec{O M}, \vec{O N}$ .

b) Biểu thị vectơ $\vec{M N}$ theo các vectơ $\vec{O M}, \vec{O N}$ và tìm tọa độ của $\vec{M N}$

c) Tìm độ dài của vectơ $\vec{M N}$

a) Ta có M(x; y) nên vectơ $\vec{O M}$ có toạ độ (x; y).

N(x'; y') nên vectơ $\vec{O N}$ có toạ độ (x'; y').

b) Ta có: $\vec{M N} = \vec{O N} - \vec{O M}$ (quy tắc ba điểm)

Mà tọa độ của vectơ $\vec{O N} - \vec{O M}$ là (x' – x; y' – y).

Vậy $\vec{M N} = (x' - x; y' - y) .$

c) Độ dài của vectơ $\vec{M N}$ là $|\vec{M N}| = \sqrt{{(x' - x)}^{2} + {(y' - y)}^{2}} .$

Giải Toán 10 trang 63 Tập 1

Luyện tập 2 trang 63 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).

a) Các điểm O, A, B có thẳng hàng hay không?

b) Tìm điểm M(x;y) để OABM là một hình bình hành.

a) Ta có: A(2; 1) suy ra $\vec{O A} = (2; 1)$

B(3; 3) suy ra $\vec{O B} = (3; 3)$

Hai vectơ $\vec{O A} = (2; 1), \vec{O B} = (3; 3)$ không cùng phương (vì $\frac{2}{3} \neq \frac{1}{3}$ ).

Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.

Vậy ba điểm O, A, B không thẳng hàng.

b) Các điểm O, A, B không thẳng hàng nên tứ giác OABM là hình bình hành khi và chỉ khi $\vec{O A} = \vec{M B}$

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3) (ảnh 2)

Ta có: $\vec{O A} = (2; 1), \vec{M B} = (3 - x; 3 - y)$ nên

$\vec{O A} = \vec{M B} \Leftrightarrow \{\begin{cases} 2 = 3 - x \\ 1 = 3 - y \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases} \Rightarrow M (1; 2) .$

Vậy điểm cần tìm là M(1;2).

Giải Toán 10 trang 64 Tập 1

Vận dụng trang 64 Toán 10 Tập 1: Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ dự báo.

Trong 12 giờ, tâm bão được dự báo di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3). Gọi tọa độ của M là (x;y). Bạn hãy tìm mối liên hệ giữa hai vectơ $\vec{A M}$ và $\vec{A B}$ rồi thể hiện mối quan hệ đó theo tọa độ để tìm x; y.

Do bão di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3) nên điểm M thuộc đoạn thẳng AB.

Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ (ảnh 1)

Theo dự báo, tại thời điểm 9 giờ thì tâm bão đã đi được một khoảng AM là: $\frac{A M}{A B} = \frac{9}{12} = \frac{3}{4}$

Hay $A M = \frac{3}{4} A B$

Vectơ $\vec{A M}$ cùng hướng với vectơ $\vec{A B}$ và $A M = \frac{3}{4} A B$ nên $\vec{A M} = \frac{3}{4} \vec{A B}$

Ta có: A(13,8; 108,3); B(14,1; 106,3); M(x; y)

Suy ra $\vec{A M} = (x - 13, 8; y - 108, 3), \vec{A B} = (0, 3; - 2)$

Ta có: $\vec{A M} = \frac{3}{4} \vec{A B}$

$\Leftrightarrow \{\begin{cases} x - 13, 8 = \frac{3}{4} .0, 3 \\ y - 108, 3 = \frac{3}{4} . (- 2) \end{cases} \Leftrightarrow \{\begin{cases} x = 0, 3. \frac{3}{4} + 13, 8 \\ y = - 2. \frac{3}{4} + 108, 3 \end{cases}$

$\Rightarrow \{\begin{cases} x = 14, 025 \\ y = 106, 8 \end{cases} \Rightarrow M (14, 025; 106, 8)$

Vậy ở thời điểm 9 giờ tâm bão là điểm M ở vị trí M(14,025; 106,8).

Bài tập

Giải Toán 10 trang 65 Tập 1

Bài 4.16 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2).

a) Tính độ dài của các đoạn thẳng OM, ON, MN.

b) Chứng minh rằng tam giác OMN vuông cân.

a) Ta có:

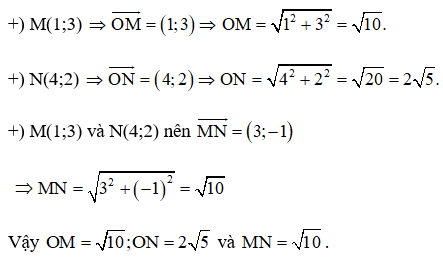
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2) (ảnh 1)

b) Xét tam giác OMN, có: $O M = M N (= \sqrt{10})$ suy ra tam giác OMN cân tại M. (1)

Ta có:

$O N^{2} = {(2 \sqrt{5})}^{2} = 20; O M^{2} + M N^{2} = {(\sqrt{10})}^{2} + {(\sqrt{10})}^{2} = 20$

$\Rightarrow O N^{2} = O M^{2} + M N^{2}$

Theo định lí Pythagore đảo suy ra tam giác OMN vuông tại M. (2)

Từ (1) và (2) suy ra tam giác OMN vuông cân tại M.

Vậy tam giác OMN vuông cân tại M.

Bài 4.17 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các vectơ $\vec{a} = 3 \vec{i} - 2 \vec{j};$ $\vec{b} = (4; - 1)$ và các điểm M(‒3;6), N(3;‒3).

a) Tìm mối liên hệ giữa các vectơ $\vec{M N}$ và $2 \vec{a} - \vec{b} .$

b) Các điểm O, M, N có thẳng hàng hay không?

c) Tìm điểm P(x;y) để OMNP là hình bình hành.

a) Ta có:

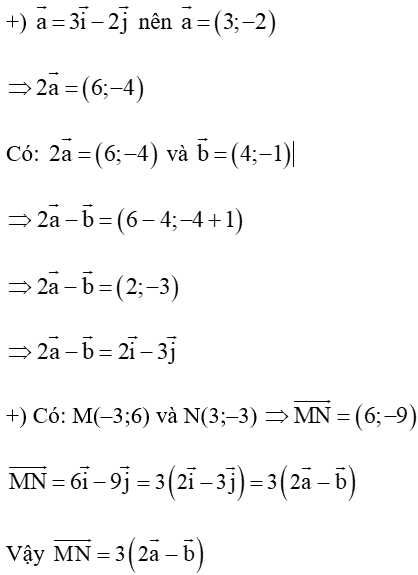
Giải Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

b) Ta có

+ M(-3; 6) $\Rightarrow \vec{O M} = (- 3; 6)$

+) N(3;‒3) $\Rightarrow \vec{O N} = (3; - 3)$

Hai vectơ $\vec{O M} = (- 3; 6), \vec{O N} = (3; - 3)$ không cùng phương (vì $\frac{- 3}{3} \neq \frac{6}{- 3}$ ).

Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.

Vậy ba điểm O, M, N không thẳng hàng.

Trong mặt phẳng tọa độ Oxy, cho các vectơ a = 3i - 2j; veco b(4; -1) (ảnh 1)

Các điểm O, M, N không thẳng hàng, tứ giác OMNP là hình bình hành khi và chỉ khi $\vec{O M} = \vec{P N}$

Ta có: M(‒3;6); N(3;‒3) và P(x; y)

$\Rightarrow \vec{O M} = (- 3; 6), \vec{P N} = (3 - x; - 3 - y)$

Do đó $\vec{O M} = \vec{P N}$

$\Leftrightarrow \{\begin{cases} - 3 = 3 - x \\ 6 = - 3 - y \end{cases} \Leftrightarrow \{\begin{cases} x = 6 \\ y = - 9 \end{cases} \Rightarrow P (6; - 9) .$

Vậy điểm cần tìm là P(6;‒9).

Bài 4.18 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(‒3;2).

a) Chứng minh rằng ABC là ba đỉnh của một tam giác.

b) Tìm tọa độ trung điểm M của đoạn thẳng AB.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD.

a) Ta có: A(1;3), B(2;4), C(‒3;2).

Suy ra: $\vec{A B} = (1; 1), \vec{B C} = (- 5; - 2)$

Hai vectơ $\vec{A B} = (1; 1), \vec{B C} = (- 5; - 2)$ không cùng phương (vì $\frac{1}{- 5} \neq \frac{1}{- 2}$ ).

Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.

Vậy ba điểm A, B, C không thẳng hàng.

Vậy ba điểm A, B, C là ba đỉnh của một tam giác.

b) Gọi M(x1;y1) là trung điểm của đoạn thẳng AB với A(1;3) và B(2;4).

Khi đó ta có:

$\{\begin{cases} x_{1} = \frac{1 + 2}{2} \\ y_{1} = \frac{3 + 4}{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \frac{3}{2} \\ y_{1} = \frac{7}{2} \end{cases} \Rightarrow M (\frac{3}{2}; \frac{7}{2}) .$

Vậy $M (\frac{3}{2}; \frac{7}{2})$ là trung điểm của đoạn thẳng AB

c) Gọi G(x2;y2) là trọng tâm của tam giác ABC với A(1;3), B(2;4) và C(‒3;2).

Khi đó ta có:

$\{\begin{cases} x_{2} = \frac{1 + 2 + (- 3)}{3} \\ y_{2} = \frac{3 + 4 + 2}{3} \end{cases} \Leftrightarrow \{\begin{cases} x_{2} = 0 \\ y_{2} = 3 \end{cases} \Rightarrow G (0; 3) .$

Vậy G(0;3) là trọng tâm của tam giác ABC.

d) Để O(0;0) là tọa độ trọng tâm tam giác ABD với A(1;3), B(2;4) và D(x,y) thì:

$\{\begin{cases} 0 = \frac{1 + 2 + x}{3} \\ 0 = \frac{3 + 4 + y}{3} \end{cases} \Leftrightarrow \{\begin{cases} x + 3 = 0 \\ y + 7 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = - 3 \\ y = - 7 \end{cases} \Rightarrow D (- 3; - 7)$

Vậy D(‒3;‒7) thì O(0;0) là trọng tâm tam giác ABD.

Bài 4.19 trang 65 Toán 10 tập 1: Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(1;2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ $\vec{v} = (3; 4) .$ Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.

Gọi B(x; y) là vị trí của tàu thủy trên mặt phẳng toạ độ sau khi khởi hành 1,5 giờ.

Tàu khởi hành từ vị trí A chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ $\vec{v} = (3; 4)$ , sau 1,5 giờ thì tàu thuỷ đến B nên $\vec{A B} = 1, 5 \vec{v}$

Mà A(1;2); B(x; y) nên $\vec{A B} = (x - 1; y - 2)$

Khi đó: $\vec{A B} = 1, 5 \vec{v}$

$\Leftrightarrow \{\begin{cases} x - 1 = 1, 5.3 \\ y - 2 = 1, 5.4 \end{cases} \Leftrightarrow \{\begin{cases} x = 1, 5.3 + 1 \\ y = 1, 5.4 + 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 5, 5 \\ y = 8 \end{cases} \Rightarrow B (5, 5; 8)$

Vậy sau khi khởi hành 1,5 giờ thì tàu thủy đến được vị trí B(5,5; 8).

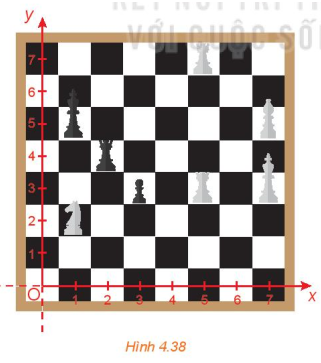
Bài 4.20 trang 65 Toán 10 Tập 1: Trong Hình 4.38, quân mã đang vị trí có tọa độ (1;2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?

Cách di chuyển của quân mã là đi theo hình chữ L, mỗi nước đi gồm tồng cộng 3 ô (tiến 1 ô rồi quẹo trái/ phải 2 ô và ngược lại hoặc tiến 2 ô rồi quẹo trái/ phải 1 ô và ngược lại) nên quân mã có thể đi đến các vị trí A, B, C, D, E và O trên bàn cờ như hình dưới đây:

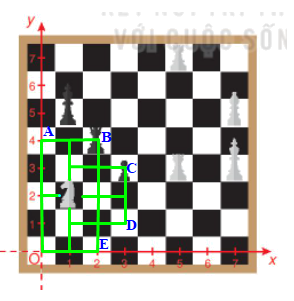
Trong Hình 4.38, quân mã đang vị trí có tọa độ (1;2) (ảnh 1)

Tọa độ của các vị trí đó là: O(0;0), A(0;4), B(2;4), C(3;3), D(3;1), E(2;0).

Vậy sau một nước đi, quân mã có thể đến các vị trí O(0;0), A(0;4), B(2;4), C(3;3), D(3;1), E(2;0).

1 195 lượt xem

Bài trước

Bài sau

Giải Toán 10 (Kết nối tri thức) Bài 10: Vectơ trong mặt phẳng tọa độ

Mở đầu