Câu hỏi:
121 lượt xemGiải Toán 10 trang 64 Tập 1
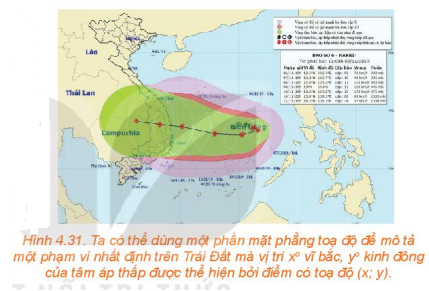
Vận dụng trang 64 Toán 10 Tập 1: Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ dự báo.
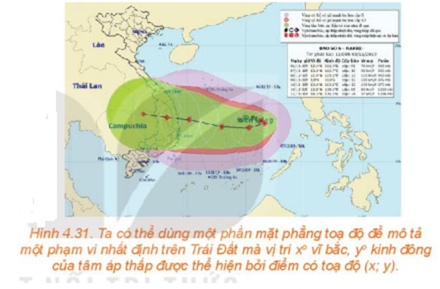
Trong 12 giờ, tâm bão được dự báo di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3). Gọi tọa độ của M là (x;y). Bạn hãy tìm mối liên hệ giữa hai vectơ và rồi thể hiện mối quan hệ đó theo tọa độ để tìm x; y.
Lời giải
Hướng dẫn giải:
Lời giải
Do bão di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3) nên điểm M thuộc đoạn thẳng AB.

Theo dự báo, tại thời điểm 9 giờ thì tâm bão đã đi được một khoảng AM là:
Hay
Vectơ cùng hướng với vectơ và nên
Ta có: A(13,8; 108,3); B(14,1; 106,3); M(x; y)
Suy ra
Ta có:
Vậy ở thời điểm 9 giờ tâm bão là điểm M ở vị trí M(14,025; 106,8).