Giải Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.

Giải bài tập Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. 

A.  Câu hỏi

 Giải Toán 10 trang 36 Tập 2

 Hoạt động 1 trang 36 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho hai đường thẳng

∆1: x – 2y + 3 = 0

∆2: 3x – y – 1 = 0

a) Điểm M(1; 2) có thuộc hai đường thẳng nói trên hay không?

b) Giải hệ $\left\{\begin{array}{l}x-2y+3=0\\ 3x-y-1=0\end{array}\right.$

c) Chỉ ra mối quan hệ giữa toạ độ giao điểm của ∆1 và ∆2 với nghiệm của hệ phương trình trên.

a) Thay toạ độ điểm M(1; 2) vào phương trình đường thẳng ∆1: x – 2y + 3 = 0 ta được   1 – 2.2 + 3 = 0 là mệnh đề đúng nên điểm M thuộc đường thẳng ∆1.

Thay toạ độ điểm M(1; 2) vào phương trình đường thẳng ∆2: 3x – y – 1 = 0 ta được   3.1 – 2 – 1= 0 là mệnh đề đúng nên điểm M thuộc đường thẳng ∆2.

Vậy M(1; 2) thuộc đường thẳng ∆1 và ∆2 hay M(1; 2) là giao điểm của hai đường thẳng ∆1; ∆2.

b) Xét hệ phương trình:$\left\{\begin{array}{l}x-2y+3=0\\ 3x-y-1=0\end{array}\right.$ ⇔$\left\{\begin{array}{l}3x-6y+9=0\left(1\right)\\ 3x-y-1=0\left(2\right)\end{array}\right.$

Trừ  phương trình (1) cho phương trình (2) vế theo vế ta được:

– 5y + 10 = 0

⇔ 5y = 10

⇔ y = 10 : 5 = 2

Thay y = 2 vào phương trình x – 2y + 3 = 0 ta được: x – 2.2 + 3 = 0

⇔ x – 4 + 3 = 0

⇔ x – 1 = 0

⇔ x  = 1

Vậy nghiệm của hệ phương trình là (2; 1).

c) Toạ độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình $\left\{\begin{array}{l}x-2y+3=0\\ 3x-y-1=0\end{array}\right.$

​Giải Toán 10 trang 37 Tập 2

 Luyện tập 1 trang 37 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:

a) ∆1: x + 4y – 3 = 0 và ∆2: x – 4y – 3 = 0;

b) ∆1: x + 2y – $\sqrt{5}$ = 0 và ∆2: 2x + 4y – 3$\sqrt{5}$ = 0.

a) Đường thẳng ∆1 có vectơ pháp tuyến $\overrightarrow{n_1}$(1; 4).

Đường thẳng ∆2 có vectơ pháp tuyến $\overrightarrow{n_2}$(1; -4).

Vì $\frac{1}{1}\ne \frac{4}{-4}$nên $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ là hai vectơ không cùng phương, do đó: ∆1 và ∆2 cắt nhau.

b) Đường thẳng ∆1 có vectơ pháp tuyến $\overrightarrow{n_1}$(1; 2)

Đường thẳng ∆2 có vectơ pháp tuyến $\overrightarrow{n_2}$(2; 4)

Vì $\overrightarrow{n_2}$= 2$\overrightarrow{n_1}$ nên $\overrightarrow{n_1}$; $\overrightarrow{n_2}$ là hai vectơ cùng phương nên ∆1 và ∆2 song song hoặc trùng nhau

Mặt khác, thay điểm A($\sqrt{5}$; 0) vào phương trình đường thẳng ∆1 ta có:$\sqrt{5}$ + 2.0 –$\sqrt{5}$= 0, do đó: điểm A($\sqrt{5}$; 0) thuộc đường thẳng ∆1.

Thay điểm A($\sqrt{5}$; 0) vào phương trình đường thẳng ∆2 ta có: 2$\sqrt{5}$ + 4.0 – 3$\sqrt{5}$= -$\sqrt{5}$≠ 0, do đó: điểm A($\sqrt{5}$; 0) không thuộc đường thẳng ∆2.  

Vậy ∆1 và ∆2 là hai đường thẳng song song.

​Hoạt động 2 trang 37 Toán 10 Tập 2: Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mỗi quan hệ gì với nhau?

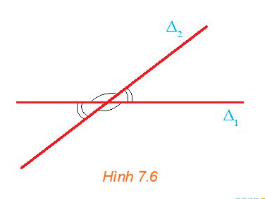
Hai đường thẳng ∆1 và ∆2 cắt nhau tại điểm A và tạo thành bốn góc lần lượt là $\widehat{A_1},\widehat{A_2},\widehat{A_3},\widehat{A_4}$ như hình vẽ:

 

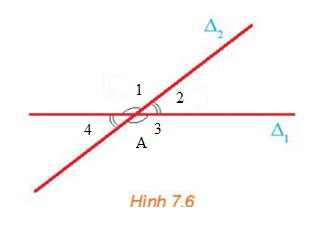
Ta thấy:

+) $\widehat{A_1}$ và $\widehat{A_3}$, $\widehat{A_2}$ và $\widehat{A_4}$ là các cặp góc đối đỉnh.

⇒ $\widehat{A_1}$ = $\widehat{A_3}$, $\widehat{A_2}$ = $\widehat{A_4}$

+) $\widehat{A_1}$ +  $\widehat{A_2}$ = 180° (hai góc kề bù)

$\widehat{A_3}$ + $\widehat{A_4}$ = 180° (hai góc kề bù)

$\widehat{A_1}$ +  $\widehat{A_4}$ = 180° (hai góc kề bù)

$\widehat{A_3}$ + $\widehat{A_2}$ = 180° (hai góc kề bù)

​Giải Toán 10 trang 38 Tập 2

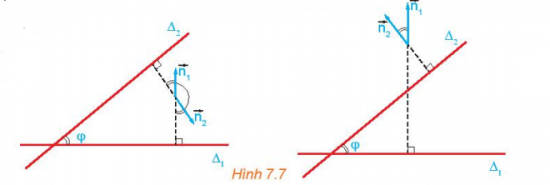
Hoạt động 3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến $\overrightarrow{n_1};\overrightarrow{n_2}$. Gọi φ là góc giữa hai đường thẳng đó (H7.7). Nêu mối quan hệ giữa:

a) góc φ và góc ($\overrightarrow{n_1};\overrightarrow{n_2}$);

b) cos φ và cos($\overrightarrow{n_1};\overrightarrow{n_2}$).

 

a)

 

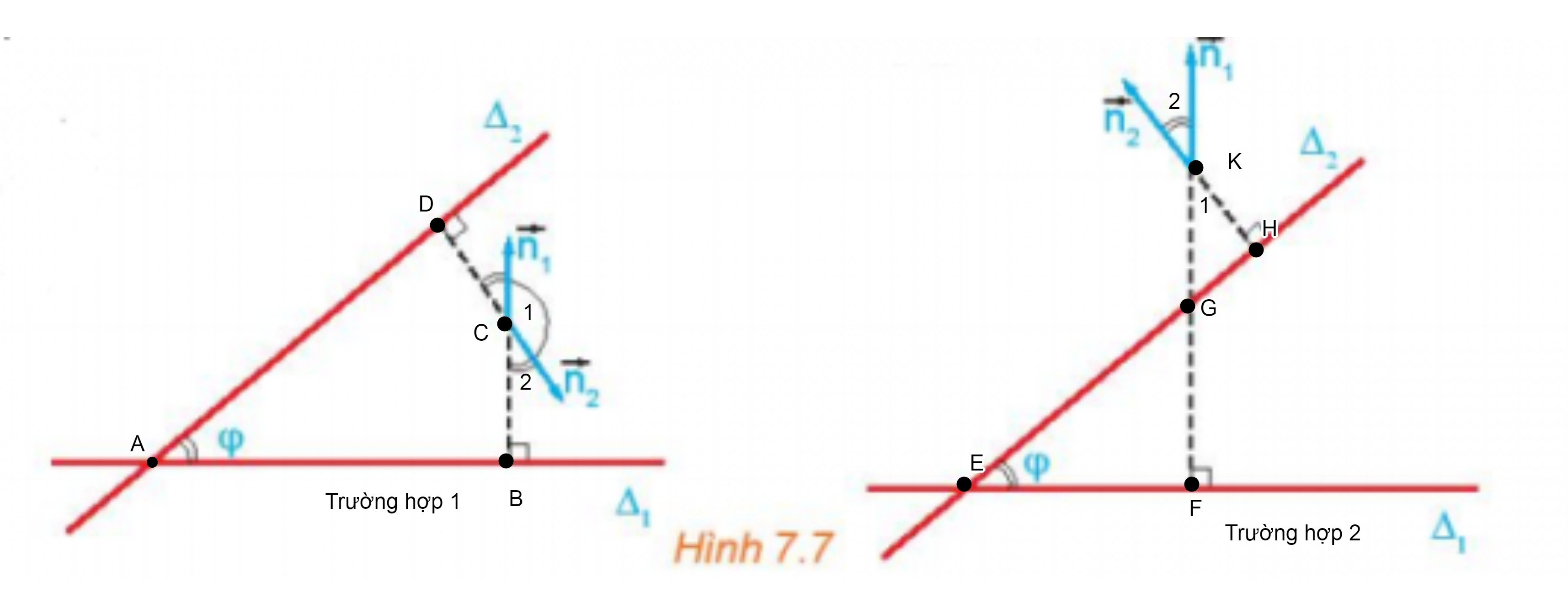
* Xét trường hợp 1:

Xét tứ giác ABCD có hai góc $\widehat{ADC;}\widehat{CBA}$ bằng 900 nên tứ giác ABCD là tứ giác nội tiếp.

Theo tính chất góc ngoài của tứ giác nội tiếp ta có : $\widehat{A}=\widehat{C_2}$= φ

Mặt khác ta có: $\widehat{C_2}$và $(\overrightarrow{n_1};\overrightarrow{n_2})$ là hai góc kề bù nên $(\overrightarrow{n_1};\overrightarrow{n_2})$= 180°– $\widehat{C_2}$= 180° – φ hay $(\overrightarrow{n_1};\overrightarrow{n_2})$ + φ = 180°

⇒ $(\overrightarrow{n_1};\overrightarrow{n_2})$ và φ là hai góc bù nhau. (1)

* Xét trường hợp 2:

Chứng minh tương tự ta có tứ giác EFHK là tứ giác nội tiếp

 

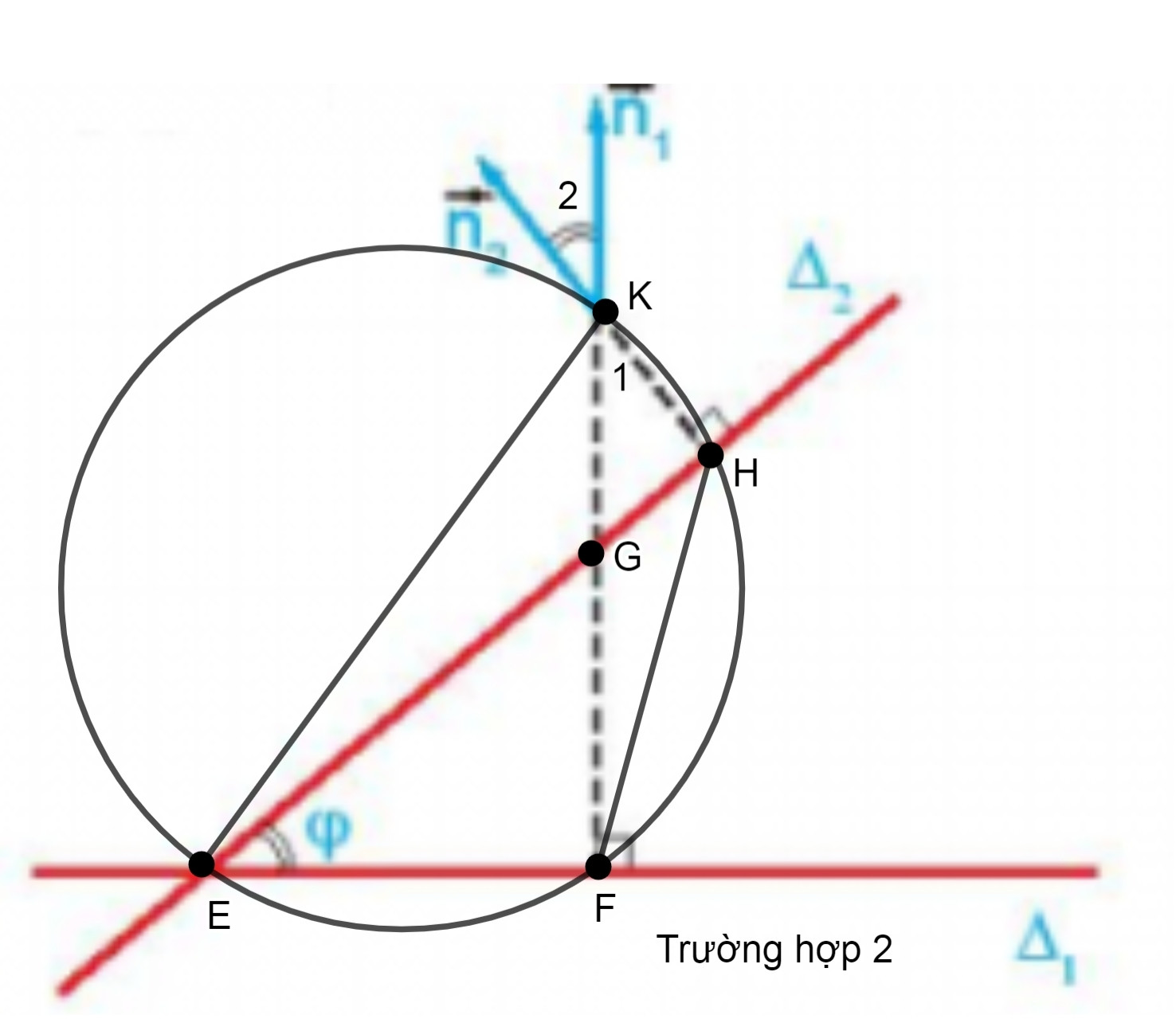
Ta có: $\widehat{FEH}$= $\widehat{K_1}$= φ (Vì hai góc nội tiếp $\widehat{FEH}$và $\widehat{K_1}$cùng chắn cung FH)

Mặt khác ta có: $\widehat{K_1}$ và $(\overrightarrow{n_1};\overrightarrow{n_2})$là hai góc đối đỉnh nên $\widehat{K_1}$= $(\overrightarrow{n_1};\overrightarrow{n_2})$

⇒ $(\overrightarrow{n_1};\overrightarrow{n_2})$ = φ. (2)

Từ (1) và (2) suy ra: $(\overrightarrow{n_1};\overrightarrow{n_2})$ = φ hoặc $(\overrightarrow{n_1};\overrightarrow{n_2})$ + φ = 180°.

Vậy mối quan hệ giữa góc $(\overrightarrow{n_1};\overrightarrow{n_2})$ và góc φ là $(\overrightarrow{n_1};\overrightarrow{n_2})$ = φ hoặc $(\overrightarrow{n_1};\overrightarrow{n_2})$ + φ = 180°.

b)

* Xét trường hợp 1: $(\overrightarrow{n_1};\overrightarrow{n_2})$= 180° – φ

Do đó cos$(\overrightarrow{n_1};\overrightarrow{n_2})$= cos(180° – φ) = -cos φ

* Xét trường hợp 2 : $(\overrightarrow{n_1};\overrightarrow{n_2})$ = φ

Ta có: cos$(\overrightarrow{n_1};\overrightarrow{n_2})$ = cosφ.

Vậy cos$(\overrightarrow{n_1};\overrightarrow{n_2})$ = |cosφ|.

​Giải Toán 10 trang 39 Tập 2

 Luyện tập 2 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1: x + 3y + 2 = 0 và $∆$2: y = 3x + 1

Phương trình đường thẳng ∆2 là y = 3x + 1 ⇔ 3x – y + 1 = 0

Đường thẳng ∆1 có vectơ pháp tuyến $\overrightarrow{n_1}$(1; 3)

Đường thẳng ∆2 có vectơ pháp tuyến $\overrightarrow{n_2}$(3; -1)

Gọi φ là góc giữa hai đường thẳng ∆1 và ∆2. Ta có:

cos φ = $\left|\cos (\overrightarrow{n_1};\overrightarrow{n_2})\right|$ = $\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$ = $\frac{\left|1.3+3.(-1)\right|}{\sqrt{1^2+3^2}.\sqrt{3^2+{(-1)}^2}}$ = 0.

⇒ $(\overrightarrow{n_1};\overrightarrow{n_2})$ = 90°.

Vậy góc giữa hai đường thẳng ∆1 và ∆2 là φ = 90°.

​Luyện tập 3 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1:$\left\{\begin{array}{l}x=2+t\\ y=1-2t\end{array}\right.$ và ∆2:$\left\{\begin{array}{l}x=1+t\text{'}\\ y=5+3t\text{'}\end{array}\right.$.

Đường thẳng ∆1 có vectơ chỉ phương là $\overrightarrow{u_1}$(1; -2) nên có vectơ pháp tuyến $\overrightarrow{n_1}$(2; 1)

Đường thẳng ∆2 có vectơ chỉ phương là $\overrightarrow{u_2}$(1; 3) nên có vectơ pháp tuyến $\overrightarrow{n_2}$(-3; 1)

Gọi φ là góc giữa hai đường thẳng ∆1 và ∆2. Ta có:

cos φ = $\left|\cos (\overrightarrow{n_1};\overrightarrow{n_2})\right|$ = $\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$ = $\frac{\left|2.(-3)+1.1\right|}{\sqrt{2^2+1^2}.\sqrt{{(-3)}^2+1^2}}$ = $\frac{5}{\sqrt{5}.\sqrt{10}}$=$\frac{1}{\sqrt{2}}$.

⇒ φ = 45°.

Vậy góc giữa hai đường thẳng $∆$1 và ∆2 là φ = 45°.

​Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0.

a) Chứng minh rằng ∆ cắt trục hoành.

b) Lập phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆.

c) Hãy chỉ ra mối quan hệ giữa ${\alpha }_{\Delta }$ và ${\alpha }_{{\Delta }_0}$

d) Gọi M là giao điểm của ∆0 với nửa đường tròn đơn vị và x0 là hoành độ của M. Tính tung độ của M theo x0 và a. Từ đó, chứng minh tan${\alpha }_{\Delta }$= a

a) Phương trình đường thẳng ∆ có dạng  ax – y + b = 0

Đường thẳng ∆ có vectơ pháp tuyến $\overrightarrow{n_{\Delta }}$(a; -1) với a ≠ 0

Trục Ox có vectơ pháp tuyến là vectơ đơn vị $\overrightarrow{j}$(0; 1)

Ta có: a.1 – (-1).0 = a ≠ 0 nên $\overrightarrow{n_{\Delta }}$ và $\overrightarrow{j}$ không cùng phương nên đường thẳng ∆ cắt trục hoành.

b) Vì đường thẳng ∆0 song song (hoặc trùng) với ∆ nên $\overrightarrow{n_{\Delta }}$và $\overrightarrow{n_{{\Delta }_0}}$cùng phương với nhau. Do đó chọn $\overrightarrow{n_{{\Delta }_0}}$(a; -1).

Phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆ là:

a(x – 0) – 1(y – 0) = 0 hay ax – y = 0.

c) Do ∆0 song song với đường thẳng ∆ nên ${\alpha }_{\Delta }$= ${\alpha }_{{\Delta }_0}$(hai góc đồng vị).

Vậy ${\alpha }_{\Delta }$= ${\alpha }_{{\Delta }_0}$.

d) Vì M là giao điểm của ∆0 với nửa đường tròn đơn vị nên toạ độ điểm M thoả mãn phương trình đường thẳng ∆0

Do đó, ta có: ax0 – y = 0 ⇒ y = ax0

⇒ M(x0; ax0)

Mặt khác ta có: tan${\alpha }_{\Delta }$= tan${\alpha }_{{\Delta }_0}$= $\frac{a{x}_0}{x_0}$ = a.

​Giải Toán 10 trang 40 Tập 2

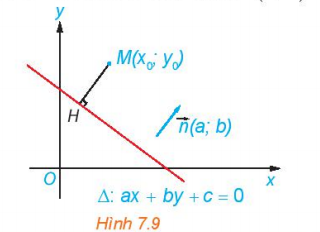
Hoạt động 4 trang 40 Toán 10 Tập 2: Cho điểm M(x0; y0) và đường thẳng ∆ : ax + by + c = 0 có vectơ pháp tuyến $\overrightarrow{n}$(a; b). Gọi H là hình chiếu vuông góc của M lên ∆ (H.7.9).

a) Chứng minh rằng $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$

b) Gỉa sử H có toạ độ (x1; y1). Chứng minh rằng:

$\overrightarrow{n}.\overrightarrow{HM}=a.(x_0-x_1)+b(y_0-y_1)={\text{ax}}_0+b{y}_0+c$

c) Chứng minh rằng HM = $\frac{\left|{\text{ax}}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$

 

a) Ta có: $\overrightarrow{n}.\overrightarrow{HM}$= $\left|\overrightarrow{n}\right|.\left|\overrightarrow{MH}\right|.\cos (\overrightarrow{n};\overrightarrow{HM})$=$\sqrt{a^2+b^2}.MH.\cos (\overrightarrow{n};\overrightarrow{HM})$

Mà $\overrightarrow{n}$ và $\overrightarrow{HM}$ là hai vectơ cùng phương (vì cùng vuông góc với ∆) nên $(\overrightarrow{n};\overrightarrow{HM})$= 00

Do đó, $\overrightarrow{n}.\overrightarrow{HM}$= $\sqrt{a^2+b^2}.MH.\cos 0^0$= $\sqrt{a^2+b^2}.MH$.

Vậy $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$(*) (đpcm)

b) Ta có: $\overrightarrow{HM}$= ( x0 – x1; y0 – y1)

Mặt khác, ta có: $\overrightarrow{n}.\overrightarrow{HM}$= a.(x0 – x1) + b.(y0 – y1)

                                     = ax0 – ax1 + by0 – by1

      = ax0 + by0 – ax1– by1 (1)

Thoe giả thiết ta có điểm H thuộc đường thẳng ∆ nên ax1 + by1 + c = 0

                                                                                     ⇒ – ax1 – by1 = c (2)

Thay (2) và (1) ta được: $\overrightarrow{n}.\overrightarrow{HM}$= a.(x0 – x1) + b.(y0 – y1) = ax0 + by0 + c (đpcm)

 Hay $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\left|a{x}_0+b{y}_0+c\right|$ (**)

c) Từ (*) và (**) ta có: $\sqrt{a^2+b^2}.MH$ = $\left|a{x}_0+b{y}_0+c\right|$ ( = $\left|\overrightarrow{n}.\overrightarrow{HM}\right|$).

⇒ MH = $\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$(đpcm).

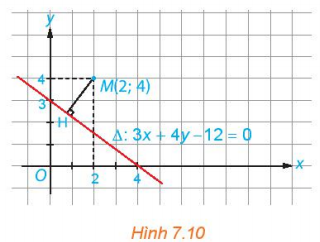
​Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4.

 

Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ là MH = 2 (đơn vị độ dài).

Kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4 vì ở cả Ví dụ 4 và bài trải nghiệm thì đều tính khoảng cách từ điểm M (2; 4) đến đường thẳng ∆: 3x + 4y – 12 = 0.

​Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng ∆: $\left\{\begin{array}{l}x=5+3t\\ y=-5-4t\end{array}\right.$$\left\{\begin{array}{l}\end{array}\right.$

Đường thẳng ∆ có vectơ chỉ phương $\overrightarrow{u}$(3; -4). Do đó, vectơ pháp tuyến của ∆ là: $\overrightarrow{n}$(4; 3).

Lấy điểm A(5; -5) thuộc ∆.

Ta có phương trình tổng quát của đường thẳng ∆ là:

4(x – 5) + 3(y + 5) = 0

⇔ 4x – 20 + 3y + 15 = 0 hay 4x + 3y – 5 = 0

Khi đó khoảng cách từ điểm M(1; 2) đến đường thẳng ∆ là :

d(M; ∆) = $\frac{\left|4.1+3.2-5\right|}{\sqrt{4^2+3^2}}$= $\frac{5}{5}$ = 1.

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là 1.

​Giải Toán 10 trang 41 Tập 2

Vận dụng  trang 41 Toán 10 Tập 2: Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15m, chiều rộng AB = 12m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5m, CF = 6m (H.7.11)

a) Chọn hệ trục toạ độ Oxy, có điểm O trùng với điểm B, các tia Ox, Oy tương ứng trùng với các tia BC, BA. Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng 1m trong thực tế. Hãy xác định toạ độ của các điểm A, B, C, D, E, F và viết phương trình đường thẳng EF.

b) Nam đứng ở vị trí B câu cá có thể quăng lưỡi câu xa 10,7 m . Hỏi lưỡi câu có thể rơi vào ao nuôi vịt hay không ?                         

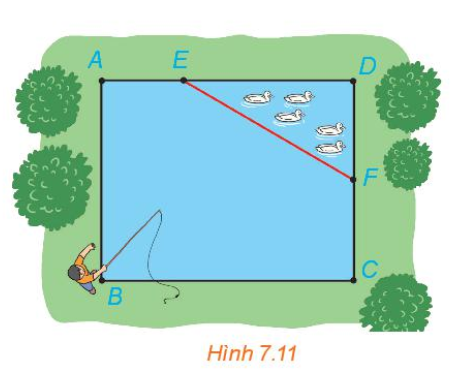
a) Đặt hệ trục tọa độ như hình vẽ:

 

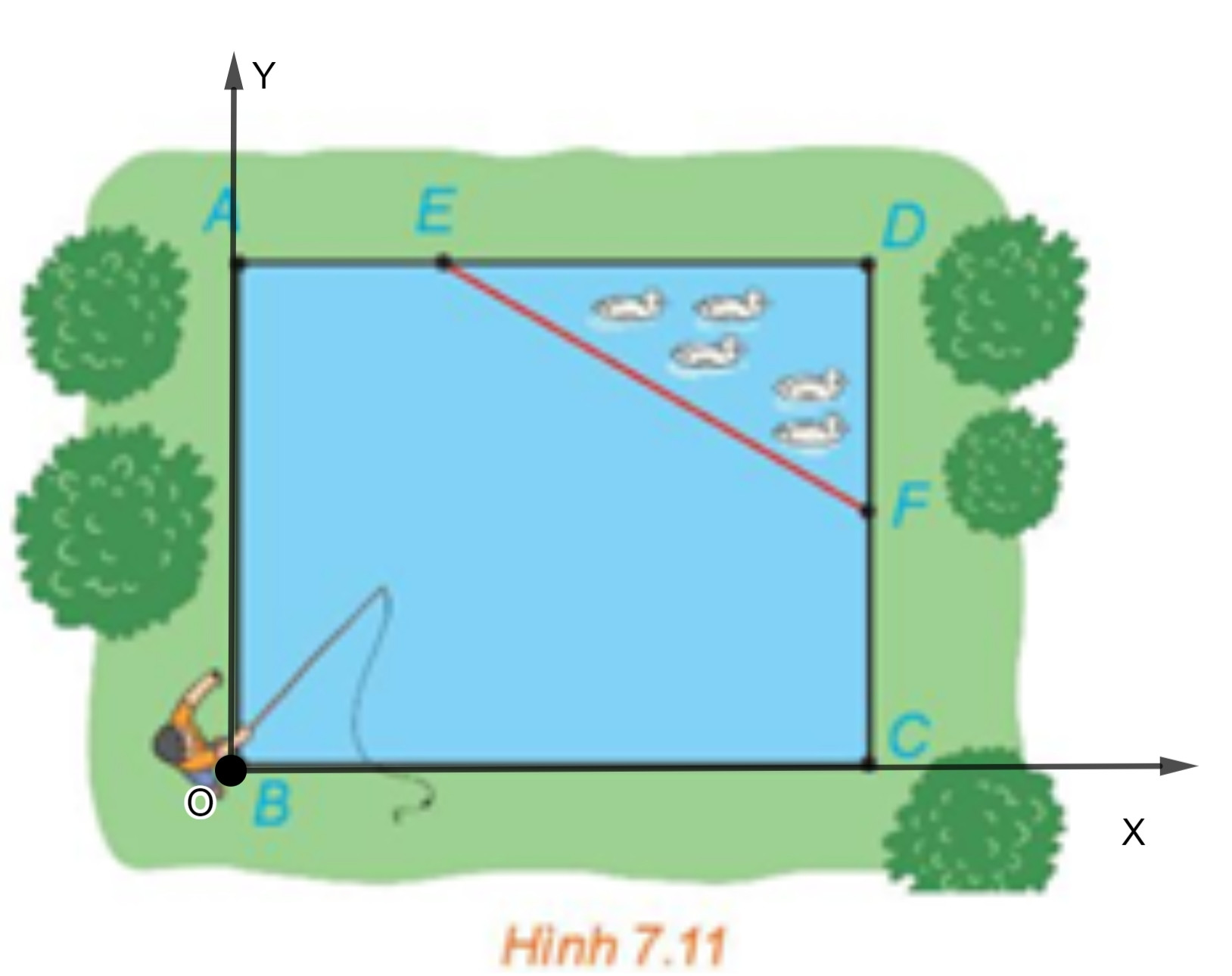
Vì ABCD là hình chữ nhật nên ta có: AD = BC = 15m, AB = DC = 12m, AE = 5m, CF  = 6m.

Khi đó, toạ các điểm lần lượt là: C(15; 0), A(0; 12), E(5; 12), D(15; 12), F(15; 6), B(0; 0).

Ta có: $\overrightarrow{EF}$= (10; -6)

Đường thẳng EF đi qua điểm  E(5; 12) và nhận $\overrightarrow{u}$= $\frac{1}{2}\overrightarrow{EF}$= (5, -3)  làm vectơ chỉ phương do đó vectơ pháp tuyến của đường thẳng EF là: $\overrightarrow{n}$(3; 5)

Suy ra phương trình tổng quát của đường thẳng EF là: 3(x – 5) + 5(y – 12) = 0 hay 3x + 5y – 75 = 0.

Vậy phương trình tổng quát của đường thẳng EF là 3x + 5y – 75 = 0.

b) Khoảng cách từ điểm B đến đường thẳng EF là:

d(B, EF) = $\frac{\left|3.0+5.0–75\right|}{\sqrt{3^2+5^2}}$= $\frac{75}{\sqrt{34}}$ ≈ 12,86 > 10,7

Vậy nếu Nam đứng ở vị trí B câu cá thì lưỡi câu không thể rơi vào ao nuôi vịt.

​B. Bài tập

 Bài 7.7 trang 41 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:

a) ∆1 : 3$\sqrt{2}$x + $\sqrt{2}$y –$\sqrt{3}$= 0 và ∆2 : 6x + 2y –$\sqrt{6}$= 0

b) d1 : x –$\sqrt{3}$y + 2 = 0 và d2 : $\sqrt{3}$x – 3y + 2 = 0

c) m1 : x – 2y + 1= 0 và m2 : 3x + y – 2 = 0

a) Vì 3$\sqrt{2}$x + $\sqrt{2}$y –$\sqrt{3}$= 0 ⇔ $\sqrt{2}$. (3$\sqrt{2}$x + $\sqrt{2}$y –$\sqrt{3}$) = 0

     ⇔  6x + 2y –$\sqrt{6}$= 0

Vậy ∆1 và ∆2 trùng nhau.

b) Đường thẳng d1 có vectơ pháp tuyến $\overrightarrow{n_1}$(1; $-\sqrt{3}$)

Đường thẳng d2 có vectơ pháp tuyến $\overrightarrow{n_2}$($\sqrt{3}$; -3)

Vì $\overrightarrow{n_2}$=$\sqrt{3}$$\overrightarrow{n_1}$nên $\overrightarrow{n_1}$; $\overrightarrow{n_2}$ là hai vectơ cùng phương nên d1 và d2 song song hoặc trùng nhau.

Mặt khác, thay điểm A(–2; 0) vào phương trình đường thẳng d1, ta có: –2 + $\sqrt{3}$.0 + 2 = 0, do đó: điểm A(–2; 0)thuộc đường thẳng d1.  

Thay điểm A(–2; 0) vào phương trình đường thẳng d2 , ta có:

$\sqrt{3}$.(–2) – 3.0 + 2 = –2$\sqrt{3}$+ 2 ≠ 0, do đó điểm A(–2; 0) không thuộc đường thẳng d2 .

Vậy d1 và d2 là hai đường thẳng song song

c) Đường thẳng m1 có vectơ pháp tuyến $\overrightarrow{n_1}$(1; -2)

Đường thẳng m2 có vectơ pháp tuyến $\overrightarrow{n_2}$(3; 1)

Vì $\frac{1}{3}\ne \frac{-2}{1}$nên $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ là hai vectơ không cùng phương , do đó: m1 và m2 cắt nhau

​Bài 7.8 trang 41 Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau:

a) ∆1 : $\sqrt{3}$x + y – 4 = 0 và ∆2 : x +$\sqrt{3}$y + 3 = 0

b) d1 : $\left\{\begin{array}{l}x=-1+2t\\ y=3+4t\end{array}\right.$ và d2 : $\left\{\begin{array}{l}x=3+s\\ y=1-3s\end{array}\right.$(t; s là các tham số)

a) Đường thẳng ∆1 có vectơ pháp tuyến $\overrightarrow{n_1}$($\sqrt{3}$; 1)

Đường thẳng ∆2 có vectơ pháp tuyến $\overrightarrow{n_2}$(1; $\sqrt{3}$)

Gọi α là góc giữa hai đường thẳng ∆1 và ∆2. Ta có:

cos α = $\left|\cos (\overrightarrow{n_1};\overrightarrow{n_2})\right|$=$\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$= $\frac{\left|\sqrt{3}.1+1.\sqrt{3}\right|}{\sqrt{{\left(\sqrt{3}\right)}^2+1^2}.\sqrt{1^2+{\left(\sqrt{3}\right)}^2}}$=$\frac{\sqrt{3}}{2}$

Vậy góc giữa hai đường thẳng ∆1 và ∆2 là α = 30°.

b)

Đường thẳng d1 có vectơ chỉ phương $\overrightarrow{u_1}$(2; 4) do đó: vectơ pháp tuyến $\overrightarrow{n_1}$(4; -2)

Đường thẳng d2 có vectơ chỉ phương $\overrightarrow{u_2}$(1; -3) do đó: vectơ pháp tuyến $\overrightarrow{n_2}$(3; 1)

Gọi β là góc giữa hai đường thẳng d1 và d2. Ta có:

cos β = $\left|\cos (\overrightarrow{n_1};\overrightarrow{n_2})\right|$=$\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$= $\frac{\left|4.3+(-2).1\right|}{\sqrt{4^2+{(-2)}^2}.\sqrt{3^2+1^2}}$=$\frac{1}{\sqrt{2}}$

Vậy góc giữa hai đường thẳng ∆1 và ∆2 là β = 45°.

​Giải Toán 10 trang 42 Tập 2

Bài 7.9 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ Oxy cho điểm A(0; –2) và đường thẳng ∆ : x + y – 4 = 0

a) Tính khoảng cách từ điểm A đến đường thẳng ∆.

b) Viết phương trình đường thẳng a đi qua điểm M(–1; 0) và song song với ∆.

c) Viết phương trình đường thẳng b đi qua điểm N(0; 3) và vuông góc với ∆.

a) Đường thẳng ∆ có vectơ pháp tuyến $\overrightarrow{n}$(1; 1)

d(A; ∆) = $\frac{\left|0-2–4\right|}{\sqrt{1^2+1^2}}$= $\frac{6}{\sqrt{2}}$= $3\sqrt{2}$.

Vậy khoảng cách từ điểm A đến đường thẳng ∆ là d(A; ∆) = $3\sqrt{2}$.

b) Đường thẳng a song song với đường thẳng ∆ nên phương trình đường thẳng a có dạng: x + y + c = 0

Vì đường thẳng a đi qua điểm M(–1; 0) nên -1 + 0 + c = 0 ⇒ c = 1

Vậy phương trình đường thẳng a là: x + y + 1 = 0.

c) Đường thẳng b vuông góc với đường thẳng ∆ nên đường thẳng b nhận vectơ chỉ phương của đường thẳng ∆ làm vectơ pháp tuyến

Ta có đường thẳng ∆ có VTCP là: $\overrightarrow{u_{\Delta }}$(1; –1) nên VTPT của đường thẳng ∆ là $\overrightarrow{n_b}$(1; –1).

Vậy phương trình đường thẳng b là: 1.(x – 0) – 1(y – 3) = 0 hay x – y + 3 = 0.

​Bài 7.10 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(–2; –1)

a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.

b) Tính diện tích ABC.

a) Ta có: $\overrightarrow{CB}$= (5; 3)

Đường thẳng BC có $\overrightarrow{CB}$là vectơ chỉ phương , do đó: vectơ pháp tuyến của đường thẳng BC là $\overrightarrow{n}$(3; –5)

Phương trình đường thẳng BC là: 3(x – 3) – 5(y – 2) = 0 hay 3x – 5y + 1 = 0

Độ dài đường cao kẻ từ đỉnh A của tam giác ABC là khoảng cách từ điểm A đến đường thẳng BC

AH = d(A; BC) = $\frac{\left|3.1–5.0+1\right|}{\sqrt{3^2+{(-5)}^2}}$= $\frac{4}{\sqrt{34}}$= $\frac{2\sqrt{34}}{17}$.

Vậy độ dài đường cao kẻ từ đỉnh A của tam giác ABC là $\frac{2\sqrt{34}}{17}$(đvđd) .

b) BC = $\sqrt{5^2+3^2}$=$\sqrt{34}$

Vậy diện tích tam giác ABC là: S = $\frac{1}{2}.AH.BC$= $\frac{1}{2}.\frac{2\sqrt{34}}{17}.\sqrt{34}$= 2 (đvdt).

​Bài 7.11 trang 42 Toán 10 Tập 2: Chứng minh hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) vuông góc với nhau khi và chỉ khi aa’ = –1

* Giả sử d vuông góc d’, ta cần chứng minh aa’ = –1

Đường thẳng d có vectơ pháp tuyến $\overrightarrow{n}$(a; –1)

Đường thẳng d’ có vectơ pháp tuyến $\overrightarrow{n^{\text{'}}}$(a’; –1)

Vì d vuông góc d’ nên $\overrightarrow{n}$.$\overrightarrow{n^{\text{'}}}$= 0

⇒ aa’ + (–1).( –1) = 0

⇔ aa’ + 1 = 0 hay aa’ = –1 (đpcm)

* Giả sử hai đường thẳng d và d’ có aa’ = –1, ta cần chứng minh d vuông góc d’

Xét tích vô hướng $\overrightarrow{n}$.$\overrightarrow{n^{\text{'}}}$= aa’ + (–1).( –1) = aa’ + 1

Mà aa’ = –1 nên $\overrightarrow{n}$.$\overrightarrow{n^{\text{'}}}$= (–1) + 1 = 0

⇒ $\overrightarrow{n}$⊥$\overrightarrow{n^{\text{'}}}$hay d ⊥ d’ (đpcm)

​Bài 7.12 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại 3 vị trí O(0; 0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh.

Gọi vị trí phát tín hiệu âm thanh là H (x; y)

Ta có:

$\overrightarrow{OH}$= (x; y) ⇒ OH = $\sqrt{x^2+y^2}$

$\overrightarrow{AH}$= (x – 1; y) ⇒ AH = $\sqrt{{(x-1)}^2+y^2}$

 $\overrightarrow{BH}$= (x – 1; y – 3) ⇒ BH = $\sqrt{{(x-1)}^2+{(y-3)}^2}$

 Vì tín hiệu nhận được tại 3 vị trí cùng 1 thời điểm nên OH = AH = BH             

Từ đó ta có hệ phương trình:

$\left\{\begin{array}{l}OH=AH\\ AH=BH\end{array}\right.$ 

⇔$\left\{\begin{array}{l}\sqrt{x^2+y^2}=\sqrt{{(x-1)}^2+y^2}\\ \sqrt{{(x-1)}^2+y^2}=\sqrt{{(x-1)}^2+{(y-3)}^2}\end{array}\right.$

⇒$\Rightarrow \left\{\begin{array}{l}{x}^{2 }+ y^{2 }= {(x-1)}^{2 }+ y^2\\ {(x-1)}^2 + y^{2 }= {(x-1)}^2 + {(y-3)}^2\end{array}\right.$

⇔$\left\{\begin{array}{l}{x}^2=x^2-2x+1\\ y^2=y^2-6y+9\end{array}\right.$

⇔$\left\{\begin{array}{l}-2x+1=0\\ -6y+9=0\end{array}\right.$

⇒$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=\frac{3}{2}\end{array}\right.$

Vậy điểm cần tìm là H $\left(\frac{1}{2};\frac{3}{2}\right)$​