Câu hỏi:
106 lượt xemGiải Toán 10 trang 40 Tập 2
Hoạt động 4 trang 40 Toán 10 Tập 2:
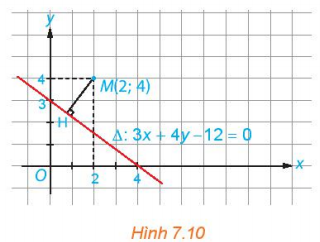
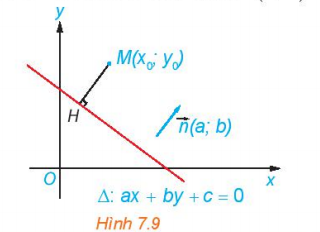
Cho điểm M(x0; y0) và đường thẳng ∆ : ax + by + c = 0 có vectơ pháp tuyến (a; b). Gọi H là hình chiếu vuông góc của M lên ∆ (H.7.9).
a) Chứng minh rằng
b) Gỉa sử H có toạ độ (x1; y1). Chứng minh rằng:
c) Chứng minh rằng HM =
Lời giải
Hướng dẫn giải:
Lời giải
a) Ta có: = =
Mà và là hai vectơ cùng phương (vì cùng vuông góc với ∆) nên = 00
Do đó, = = .
Vậy (*) (đpcm)
b) Ta có: = ( x0 – x1; y0 – y1)
Mặt khác, ta có: = a.(x0 – x1) + b.(y0 – y1)
= ax0 – ax1 + by0 – by1
= ax0 + by0 – ax1– by1 (1)
Thoe giả thiết ta có điểm H thuộc đường thẳng ∆ nên ax1 + by1 + c = 0
⇒ – ax1 – by1 = c (2)
Thay (2) và (1) ta được: = a.(x0 – x1) + b.(y0 – y1) = ax0 + by0 + c (đpcm)
Hay (**)
c) Từ (*) và (**) ta có: = ( = ).
⇒ MH = (đpcm).
Luyện tập 3 trang 39 Toán 10 Tập 2:
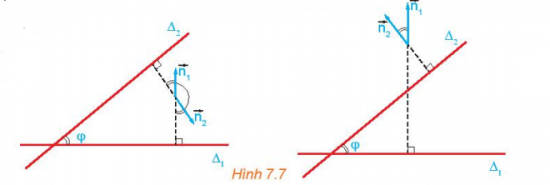
Tính góc giữa hai đường thẳng ∆1: và ∆2:.