Câu hỏi:
120 lượt xemGiải Toán 10 trang 38 Tập 2
Hoạt động 3 trang 38 Toán 10 Tập 2:
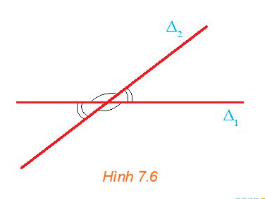
Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến . Gọi φ là góc giữa hai đường thẳng đó (H7.7). Nêu mối quan hệ giữa:
a) góc φ và góc ();
b) cos φ và cos().
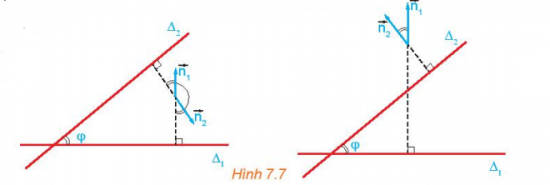
Lời giải
Hướng dẫn giải:
Lời giải
a)
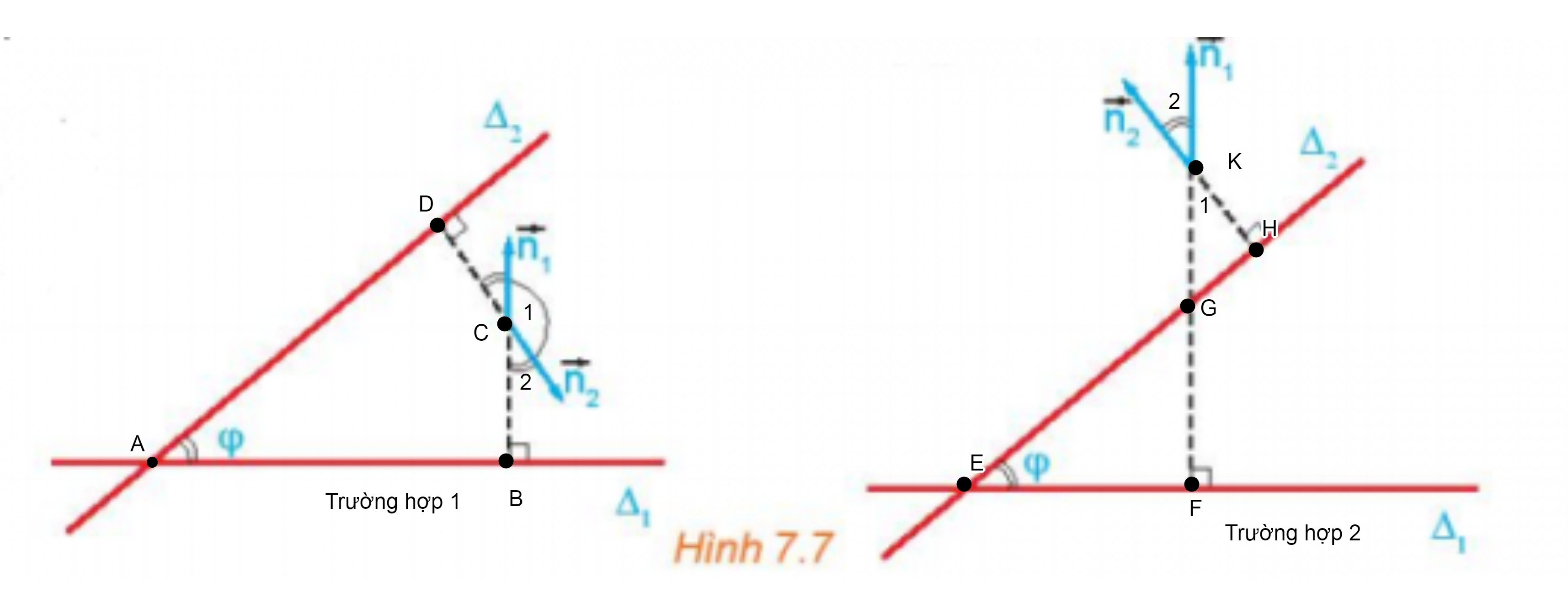
* Xét trường hợp 1:
Xét tứ giác ABCD có hai góc bằng 900 nên tứ giác ABCD là tứ giác nội tiếp.
Theo tính chất góc ngoài của tứ giác nội tiếp ta có : = φ
Mặt khác ta có: và là hai góc kề bù nên = 180°– = 180° – φ hay + φ = 180°
⇒ và φ là hai góc bù nhau. (1)
* Xét trường hợp 2:
Chứng minh tương tự ta có tứ giác EFHK là tứ giác nội tiếp
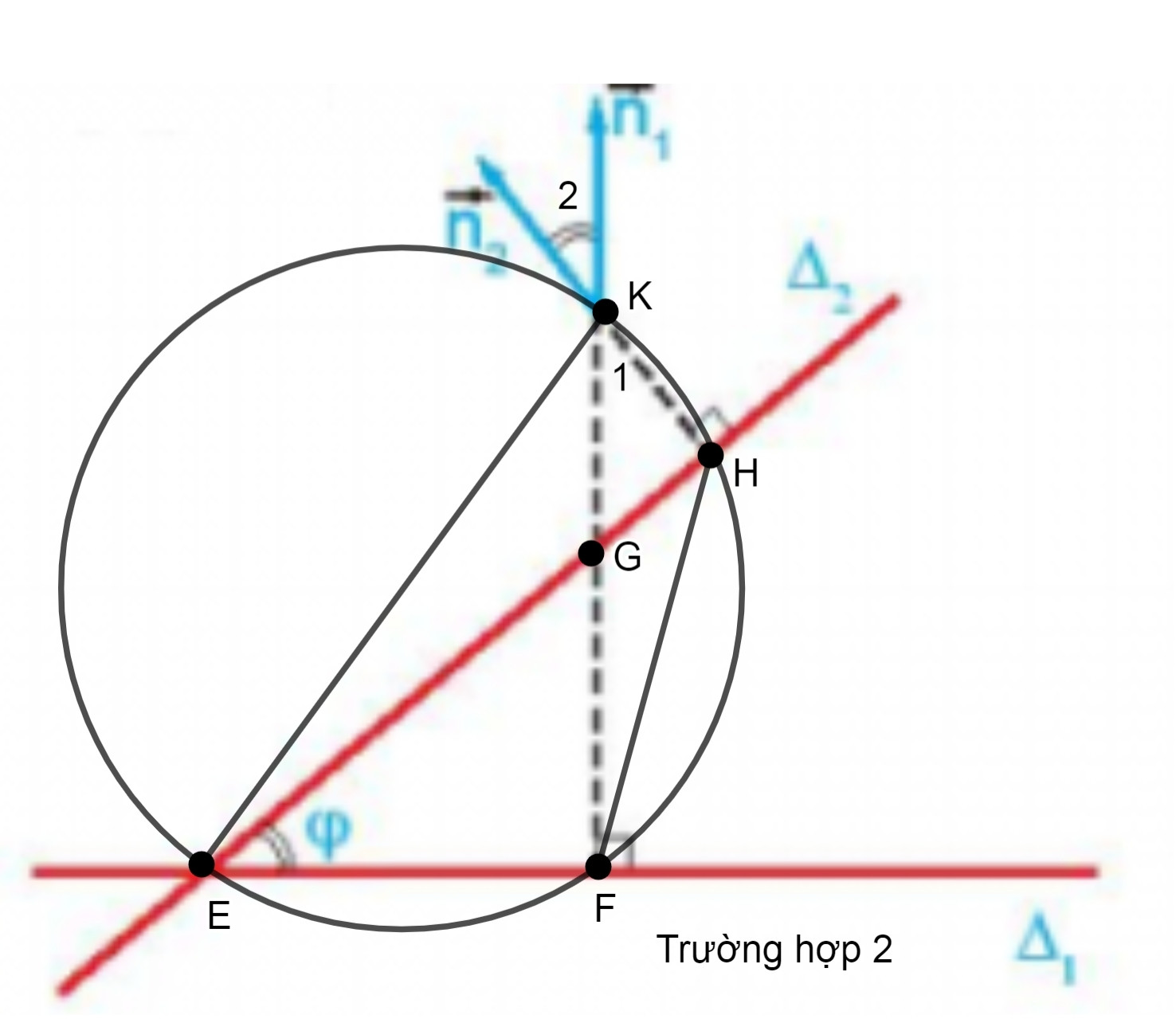
Ta có: = = φ (Vì hai góc nội tiếp và cùng chắn cung FH)
Mặt khác ta có: và là hai góc đối đỉnh nên =
⇒ = φ. (2)
Từ (1) và (2) suy ra: = φ hoặc + φ = 180°.
Vậy mối quan hệ giữa góc và góc φ là = φ hoặc + φ = 180°.
b)
* Xét trường hợp 1: = 180° – φ
Do đó cos= cos(180° – φ) = -cos φ
* Xét trường hợp 2 : = φ
Ta có: cos = cosφ.
Vậy cos = |cosφ|.
Luyện tập 3 trang 39 Toán 10 Tập 2:
Tính góc giữa hai đường thẳng ∆1: và ∆2:.