Câu hỏi:
112 lượt xemGiải bài tập Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.
A. Câu hỏi
Giải Toán 10 trang 36 Tập 2
Hoạt động 1 trang 36 Toán 10 Tập 2:
Trong mặt phẳng toạ độ, cho hai đường thẳng
∆1: x – 2y + 3 = 0
∆2: 3x – y – 1 = 0
a) Điểm M(1; 2) có thuộc hai đường thẳng nói trên hay không?
b) Giải hệ ![]()
c) Chỉ ra mối quan hệ giữa toạ độ giao điểm của ∆1 và ∆2 với nghiệm của hệ phương trình trên.
Lời giải
Hướng dẫn giải:
Lời giải:
a) Thay toạ độ điểm M(1; 2) vào phương trình đường thẳng ∆1: x – 2y + 3 = 0 ta được 1 – 2.2 + 3 = 0 là mệnh đề đúng nên điểm M thuộc đường thẳng ∆1.
Thay toạ độ điểm M(1; 2) vào phương trình đường thẳng ∆2: 3x – y – 1 = 0 ta được 3.1 – 2 – 1= 0 là mệnh đề đúng nên điểm M thuộc đường thẳng ∆2.
Vậy M(1; 2) thuộc đường thẳng ∆1 và ∆2 hay M(1; 2) là giao điểm của hai đường thẳng ∆1; ∆2.
b) Xét hệ phương trình: ⇔
Trừ phương trình (1) cho phương trình (2) vế theo vế ta được:
– 5y + 10 = 0
⇔ 5y = 10
⇔ y = 10 : 5 = 2
Thay y = 2 vào phương trình x – 2y + 3 = 0 ta được: x – 2.2 + 3 = 0
⇔ x – 4 + 3 = 0
⇔ x – 1 = 0
⇔ x = 1
Vậy nghiệm của hệ phương trình là (2; 1).
c) Toạ độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình ![]()
Luyện tập 3 trang 39 Toán 10 Tập 2:
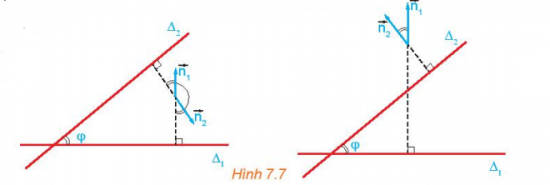
Tính góc giữa hai đường thẳng ∆1: và ∆2:.