Câu hỏi:
111 lượt xemBài 7.11 trang 42 Toán 10 Tập 2:
Chứng minh hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) vuông góc với nhau khi và chỉ khi aa’ = –1
Lời giải
Hướng dẫn giải:
Lời giải
* Giả sử d vuông góc d’, ta cần chứng minh aa’ = –1
Đường thẳng d có vectơ pháp tuyến (a; –1)
Đường thẳng d’ có vectơ pháp tuyến (a’; –1)
Vì d vuông góc d’ nên .= 0
⇒ aa’ + (–1).( –1) = 0
⇔ aa’ + 1 = 0 hay aa’ = –1 (đpcm)
* Giả sử hai đường thẳng d và d’ có aa’ = –1, ta cần chứng minh d vuông góc d’
Xét tích vô hướng .= aa’ + (–1).( –1) = aa’ + 1
Mà aa’ = –1 nên .= (–1) + 1 = 0
⇒ ⊥hay d ⊥ d’ (đpcm)
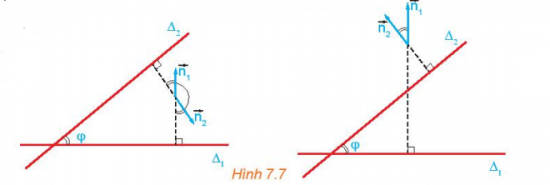
Luyện tập 3 trang 39 Toán 10 Tập 2:
Tính góc giữa hai đường thẳng ∆1: và ∆2:.