Câu hỏi:
107 lượt xemLuyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0.
a) Chứng minh rằng ∆ cắt trục hoành.
b) Lập phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆.
c) Hãy chỉ ra mối quan hệ giữa và
d) Gọi M là giao điểm của ∆0 với nửa đường tròn đơn vị và x0 là hoành độ của M. Tính tung độ của M theo x0 và a. Từ đó, chứng minh tan= a
Lời giải
Hướng dẫn giải:
Lời giải
a) Phương trình đường thẳng ∆ có dạng ax – y + b = 0
Đường thẳng ∆ có vectơ pháp tuyến (a; -1) với a ≠ 0
Trục Ox có vectơ pháp tuyến là vectơ đơn vị (0; 1)
Ta có: a.1 – (-1).0 = a ≠ 0 nên và không cùng phương nên đường thẳng ∆ cắt trục hoành.
b) Vì đường thẳng ∆0 song song (hoặc trùng) với ∆ nên và cùng phương với nhau. Do đó chọn (a; -1).
Phương trình đường thẳng ∆0 đi qua điểm O(0; 0) và song song (hoặc trùng) với ∆ là:
a(x – 0) – 1(y – 0) = 0 hay ax – y = 0.
c) Do ∆0 song song với đường thẳng ∆ nên = (hai góc đồng vị).
Vậy = .
d) Vì M là giao điểm của ∆0 với nửa đường tròn đơn vị nên toạ độ điểm M thoả mãn phương trình đường thẳng ∆0
Do đó, ta có: ax0 – y = 0 ⇒ y = ax0
⇒ M(x0; ax0)
Mặt khác ta có: tan= tan= = a.
Luyện tập 3 trang 39 Toán 10 Tập 2:
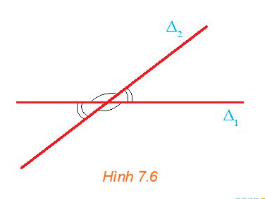
Tính góc giữa hai đường thẳng ∆1: và ∆2:.