Câu hỏi:
127 lượt xemGiải Toán 10 trang 42 Tập 2
Bài 7.9 trang 42 Toán 10 Tập 2:
Trong mặt phẳng toạ độ Oxy cho điểm A(0; –2) và đường thẳng ∆ : x + y – 4 = 0
a) Tính khoảng cách từ điểm A đến đường thẳng ∆.
b) Viết phương trình đường thẳng a đi qua điểm M(–1; 0) và song song với ∆.
c) Viết phương trình đường thẳng b đi qua điểm N(0; 3) và vuông góc với ∆.
Lời giải
Hướng dẫn giải:
Lời giải
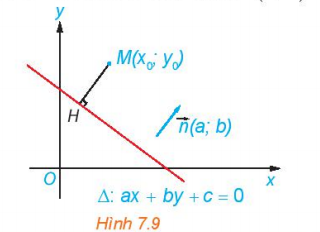
a) Đường thẳng ∆ có vectơ pháp tuyến (1; 1)
d(A; ∆) = = = .
Vậy khoảng cách từ điểm A đến đường thẳng ∆ là d(A; ∆) = .
b) Đường thẳng a song song với đường thẳng ∆ nên phương trình đường thẳng a có dạng: x + y + c = 0
Vì đường thẳng a đi qua điểm M(–1; 0) nên -1 + 0 + c = 0 ⇒ c = 1
Vậy phương trình đường thẳng a là: x + y + 1 = 0.
c) Đường thẳng b vuông góc với đường thẳng ∆ nên đường thẳng b nhận vectơ chỉ phương của đường thẳng ∆ làm vectơ pháp tuyến
Ta có đường thẳng ∆ có VTCP là: (1; –1) nên VTPT của đường thẳng ∆ là (1; –1).
Vậy phương trình đường thẳng b là: 1.(x – 0) – 1(y – 3) = 0 hay x – y + 3 = 0.
Luyện tập 3 trang 39 Toán 10 Tập 2:
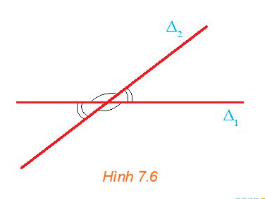
Tính góc giữa hai đường thẳng ∆1: và ∆2:.