Câu hỏi:
104 lượt xemBài 4.35 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(‒2; 5) và C(‒5; 2).
a) Tìm tọa độ của các vectơ và
b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.
Lời giải
Hướng dẫn giải:
Lời giải
a) Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: và
b) Ta có:
vuông tại B.
Do ;
.
Với A(2; 1) và C(‒5; 2) ta có:
Diện tích tam giác vuông ABC là:
(đơn vị diện tích)
Chu vi tam giác ABC là:
AB + BC + AC = (đơn vị độ dài)
c) Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có tọa độ trọng tâm G của tam giác ABC là:
Vậy tọa độ trọng tâm của tam giác ABC là:
d)
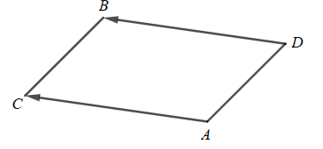
Để tứ giác BCAD là hình bình hành thì
Giả sử D(x; y) là điểm cần tìm.
Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: và
Do đó
.
Vậy với D(5;4) thì tứ giác BCAD là một hình bình hành.
Bài 4.31 trang 71 Toán 10 Tập 1: Khẳng định nào sau đây là đúng?
A.
B.
C.
D.