a) Ta có A + B = x³ + 3x + 1

Suy ra:

B = x³ + 3x + 1 - A

    = x³ + 3x + 1 - (x⁴ + x³ - 2x - 2)

    = x³ + 3x + 1 - x⁴ - x³ + 2x + 2

    = - x⁴ + (x³ - x³) + (3x + 2x) + (1 + 2)

    = - x⁴ + 5x + 3

Vậy B = -x⁴ + 5x + 3.

b) Ta có A - C = x⁵

Suy ra:

C = A - x⁵

   = x⁴ + x³ - 2x - 2 - x⁵

   = - x⁵ + x⁴ + x³ - 2x - 2

Vậy C = - x⁵ + x⁴ + x³ - 2x - 2.

c) Ta có D = (2x² - 3) . A

D = (2x² - 3) . (x⁴ + x³ - 2x - 2)

    = 2x² . (x⁴ + x³ - 2x - 2) + (-3) . (x⁴ + x³ - 2x - 2)

    = [2x² . x⁴ + 2x² . x³ + 2x² . (-2x) + 2x² . (-2)]

            + [(-3) . x⁴ + (-3) . x³ + (-3) . (-2x) + (-3) . (-2)]

    = 2x⁶ + 2x⁵ - 4x³ - 4x² - 3x⁴ - 3x³ + 6x + 6

    = 2x⁶ + 2x⁵ - 3x⁴ + (-4x³ - 3x³) - 4x² + 6x + 6

    = 2x⁶ + 2x⁵ - 3x⁴ - 7x³ - 4x² + 6x + 6

Vậy D = 2x⁶ + 2x⁵ - 3x⁴ - 7x³ - 4x² + 6x + 6.

d) Ta có A = (x + 1) . P

Suy ra P = A : (x + 1)

P = (x⁴ + x³ - 2x - 2) : (x + 1)

Đặt tính chia ta được:

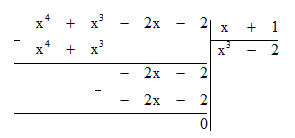
Vậy P = x³ - 2.

e) Thực hiện đặt tính chia đa thức A cho đa thức x² + 1 ta được:

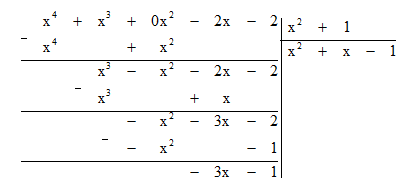
Ta thấy đa thức A chia cho đa thức x² + 1 dư -3x - 1 nên không tồn tại đa thức Q sao cho

A = (x² + 1) . Q.