Câu hỏi:
92 lượt xemLời giải
Hướng dẫn giải:
|
GT |
AB = CD, |
|
KL |
|
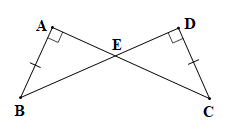
Chứng minh (hình vẽ trên):
Theo giả thiết ta có tam giác ABE vuông tại A và tam giác DCE vuông tại D.
Tam giác ABE vuông tại A nên hai góc nhọn của tam giác phụ nhau.
Tức là suy ra
Tam giác DCE vuông tại D nên hai góc nhọn của tam giác phụ nhau.
Tức là suy ra .
Mà (hai góc đối đỉnh).
Do đó hay .
Xét tam giác ABE (vuông tại A) và tam giác DCE (vuông tại D) có:
AB = DC (theo giả thiết);
(chứng minh trên).
Vậy (cạnh góc vuông – góc nhọn kề).
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 15:
Tự luận
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng
1 năm trước
126 lượt xem
