Câu hỏi:
294 lượt xemHoạt động 1 trang 50 Chuyên đề Toán 11: Cho mặt phẳng (P), điểm M, đoạn thẳng AB và đường thẳng a. Xác định hình chiếu vuông góc trên mặt phẳng (P) của:
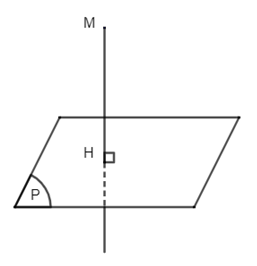
a) Điểm M;
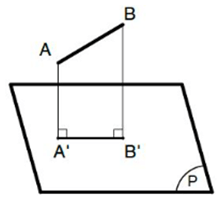
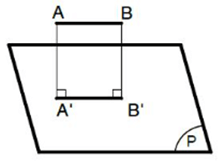
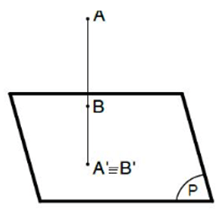
b) Đoạn thẳng AB;
c) Đường thẳng a
Lời giải
Hướng dẫn giải:
a)
+) TH1: Điểm M thuộc mặt phẳng (P) thì hình chiếu vuông góc của M lên mặt phẳng (P) là chính nó.
+) TH2: Điểm M không thuộc mặt phẳng (P).
Từ M kẻ đường thẳng vuông góc với mặt phẳng (P), đường thẳng này cắt mặt phẳng (P) tại H. Vậy H là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
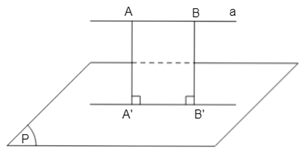
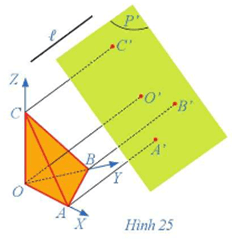
b) Tùy theo vị trí của đoạn thẳng so với mặt phẳng hình chiếu, ta có 3 trường hợp:
+) TH1: Đoạn thẳng xiên với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng không song song và có độ dài không bằng nó (A'B' < AB).
+) TH2: Đoạn thẳng song song với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng song song và có độ dài bằng nó (A'B' = AB).
+) TH3: Đoạn thẳng vuông góc với mặt phẳng hình chiếu: hình chiếu của nó là một điểm (A' ≡ B').
c)
+) TH1: Đường thẳng a nằm trong mặt phẳng (P) thì hình chiếu vuông góc của đường thẳng a trên mặt phẳng (P) là chính nó.
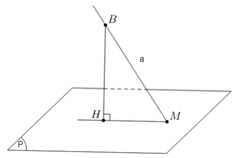
+) TH2: Đường thẳng a cắt mặt phẳng (P).
Gọi M là giao điểm của đường thẳng a và mặt phẳng (P). Lấy điểm B khác M thuộc đường thẳng a, xác định hình chiếu vuông góc H của B trên mặt phẳng (P). Khi đó hình chiếu vuông góc của đường thẳng a lên mặt phẳng (P) là đường thẳng đi qua hai điểm M và H.
Tổng quát:
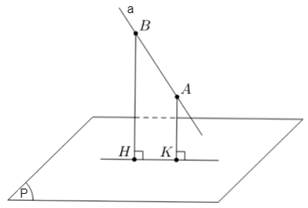
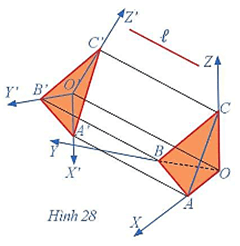
+) TH3: Đường thẳng a song song với mặt phẳng (P).
Lấy hai điểm A, B khác nhau trên đường thẳng a, xác định hình chiếu vuông góc A', B' lần lượt của A và B trên mặt phẳng (P). Khi đó hình chiếu vuông góc của đường thẳng a trên mặt phẳng (P) là đường thẳng A'B' (A'B' // a).
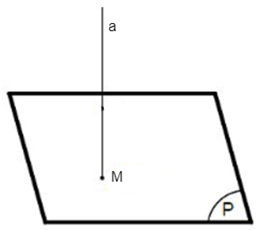
+) TH4: Đường thẳng a vuông góc với mặt phẳng (P).
Khi đó hình chiếu vuông của đường thẳng a trên mặt phẳng (P) là giao điểm M của a và (P).