Câu hỏi:
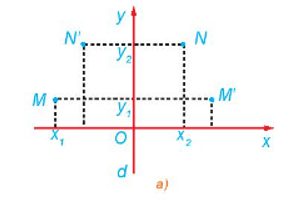
102 lượt xemCho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là (x1; y1), N có tọa độ là (x2; y2).
a) Hãy cho biết tọa độ của M', N'.
b) Tính MN2, M'N'2 theo tọa độ của các điểm tương ứng.
c) So sánh độ dài các đoạn thẳng MN, M'N'.
Lời giải
Hướng dẫn giải:
a) M' và N' lần lượt là ảnh của M và N qua phép đối xứng trục d (trục Oy).
Do đó M'(– x1; y1) và N'(– x2; y2).
b) Ta có: = (x2 – x1)2 + (y2 – y1)2
= (– x2 + x1)2 + (y2 – y1)2.
c) Ta có: (x2 – x1)2 = (x1 – x2)2 = (– x2 + x1)2.
Do đó (x2 – x1)2 + (y2 – y1)2 = (– x2 + x1)2 + (y2 – y1)2 hay MN2 = M'N'2.
Suy ra MN = M'N'.
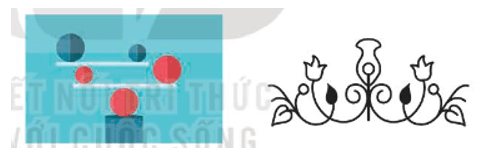
Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.
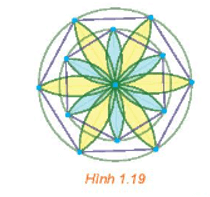
Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.