Câu hỏi:
98 lượt xemTrong mặt phẳng tọa độ Oxy, cho ∆: x + 2y – 1 = 0. Viết phương trình đường thẳng d đối xứng với ∆ qua trục Ox.
Lời giải
Hướng dẫn giải:
Đường thẳng d đối xứng với ∆ qua trục Ox hay d là ảnh của ∆ qua phép đối xứng trục Ox.
Cách 1:
Lấy hai điểm A(1; 0) và B(– 1; 1) thuộc ∆.
Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.
Khi đó A'(1; 0) và B'(– 1; – 1).
Vì d là ảnh của đường thẳng ∆ qua phép đối xứng trục Ox nên A' và B' thuộc d.
Ta có: . Suy ra .
Vậy d có phương trình là 1(x – 1) – 2(y – 0) = 0 hay x – 2y – 1 = 0.
Cách 2:
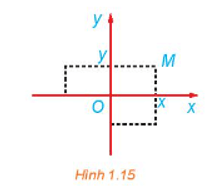
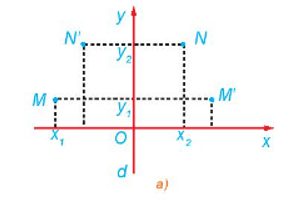
Gọi M'(x'; y') là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó x' = x và y' = – y.
Ta có: M ∈ ∆ ⇔ x + 2y – 1 = 0 ⇔ x' + 2.(– y') – 1 = 0 ⇔ x' – 2y' – 1 = 0 ⇔ M' thuộc đường thẳng d có phương trình là x – 2y – 1 = 0.
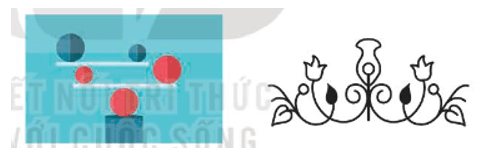
Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.
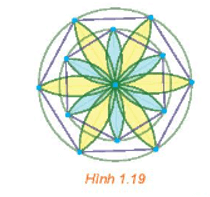
Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.