Câu hỏi:
52 lượt xemLời giải
Hướng dẫn giải:
|
GT |
Tam giác ABC, Cx là tia đối của tia CB. |
|
KL |
|
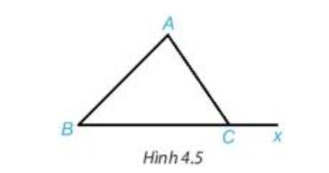
Chứng minh (Hình vẽ trên):
Theo giả thiết Cx là tia đối của tia CB nên hai góc ACB và Acx là hai góc kề bù, hay (tính chất hai góc kề bù).
Suy ra (1).
Trong tam giác ABC ta có (Định lí tổng ba góc trong một tam giác).
Suy ra (2).
Từ (1) và (2) ta có .
Vậy
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 7:
Câu 8:
Câu 9:
Tự luận
Tính các số đo x, y, z trong Hình 4.8Tính các số đo x, y, z trong Hình 4.8
1 năm trước
46 lượt xem
