Câu hỏi:
238 lượt xem Tự luận
Bài 2.12 trang 45 Chuyên đề Toán 11: a) Giả sử G là một đồ thị với n đỉnh và cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.
b) Tìm một đồ thị với n đỉnh và cạnh mà không có chu trình Hamilton.
Lời giải
Hướng dẫn giải:
a) Định lí Ore: Nếu G là một đồ thị có n đỉnh (n 3) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.
Ta có lí thuyết: Giả sử G là đồ thị đơn gồm n đỉnh và m cạnh. Nếu m \(\ge\dfrac{n^2-3n+6}{2}\) thì G là đồ thị có chu trình Hamilton.
Áp dụng vào bài toán ta được điều phải chứng minh.
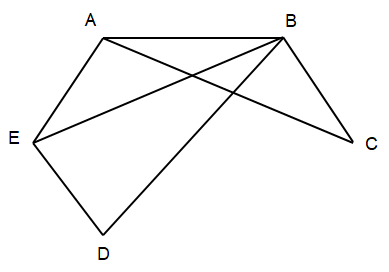
b) Ta có đồ thị sau có 5 đỉnh, 7 cạnh và đồ thị không có chu trình Hamilton.
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 12:
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 79 lượt thi