Câu hỏi:
198 lượt xemBài 2.11 trang 45 Chuyên đề Toán 11: Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn ”.
Lời giải
Hướng dẫn giải:
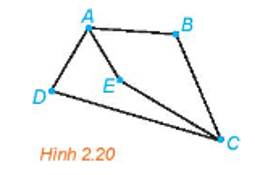
Cho đơn đồ thị G có 5 đỉnh như hình vẽ sau:
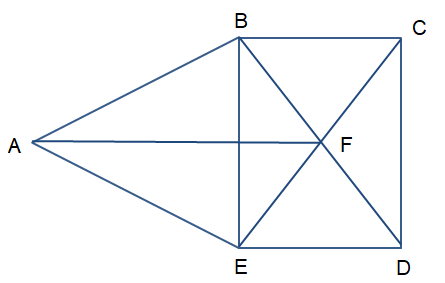
Mỗi đỉnh của đồ thị này đều có bậc là 2 hoặc 3, đều không nhỏ hơn , thỏa mãn điều kiện của định lí Dirac nếu thay điều kiện “bậc của mỗi đỉnh của đồ thị G không nhỏ hơn ” bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn ”.
Định lí Dirac là một điều kiện đủ cho sự tồn tại chu trình Hamilton, nhưng đồ thị trên lại không có chu trình Hamilton. Do vậy, đây vì ví dụ cần đưa ra để chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn ”.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 153 lượt thi