Câu hỏi:
124 lượt xemGiải Toán 10 trang 46 Tập 2
Hoạt động 2 trang 46 Toán 10 Tập 2:
Cho đường tròn (C) : (x – 1)2 + (y – 2)2 = 25 và điểm M(4; –2)
a) Chứng minh điểm M(4; –2) thuộc đường tròn (C)
b) Xác định tâm và bán kính của (C)
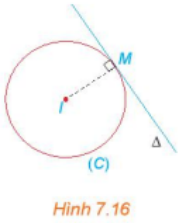
c) Gọi ∆ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ (H.7.16) . Từ đó, viết phương trình đường thẳng ∆
Lời giải
Hướng dẫn giải:
Lời giải:
a) Thay toạ độ điểm M vào phương trình đường tròn ta được :
(4 – 1)2 + (– 2 – 2)2 = 15
⇔ 32 + (– 4)2 = 25
⇔ 25 = 25 (luôn đúng).
Vậy điểm M(4; –2) thuộc đường tròn (C).
b) Đường tròn (C) : (x – 1)2 + (y – 2)2 = 25 có tâm I(1; 2) và bán kính R = 5.
c) Vì ∆ là tiếp tuyến của (C) tại M nên IM ⊥ ∆, do đó: đường thẳng ∆ có vectơ pháp tuyến là = ( 3; –4)
Vậy phương trình đường thẳng ∆ đi qua điểm M(4; –2) và có vectơ pháp tuyến = ( 3; –4) là: 3(x – 4) – 4(y + 2) = 0 hay 3x – 4y – 20 = 0.