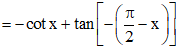Câu hỏi:
101 lượt xem Tự luận
Kết quả thu gọn của biểu thức
A=sin(π+x)+cos(π2−x)+cot(2π−x)+tan(3π2+x)?=sin?+?+cos?2−?+cot2?−?+tan3?2+? là:
A. – 2cot x.
B. 2tan x.
C. 2sin x.
D. – 2sin x.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
A=sin(π+x)+cos(π2−x)+cot(2π−x)+tan(3π2+x)?=sin?+?+cos?2−?+cot2?−?+tan3?2+?
=−sinx+sinx+cot(π+π−x)+tan(π+π2+x)=−sin?+sin?+cot?+?−?+tan?+?2+?
=cot(π−x)+tan(π2+x)=cot?−?+tan?2+?
=cot(−x)+tan(π+x−π2)=cot−?+tan?+?−?2
=−cotx−tan(π2−x)=−cot?−tan?2−?
=−cotx−cotx=−2cotx
Câu 1:
Câu 2:
Câu 3:
Tự luận
Cho tan α + cot α = 2. Khi đó, tan2 α + cot2 α bằng:
A. 8.
B. 4.
C. 16.
D. 2.
12 tháng trước
90 lượt xem
ĐỀ THI LIÊN QUAN:
-
0 câu hỏi 52 lượt thi