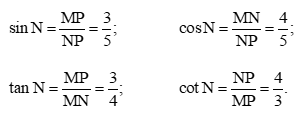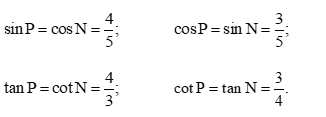Câu hỏi:
164 lượt xema) Vẽ một tam giác vuông có một góc bằng 40°. Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40°. Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thước đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.
Lời giải
Hướng dẫn giải:
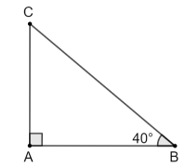
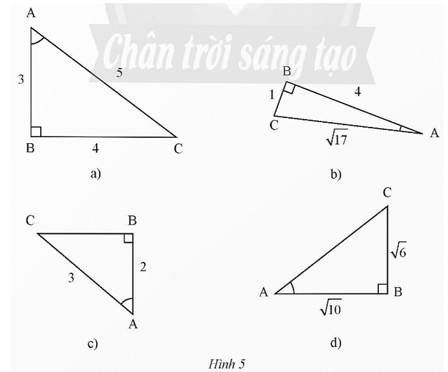
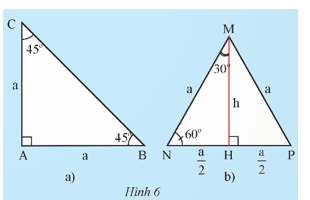
a) Vẽ tam giác vuông có một góc bằng 40°.
• Chẳng hạn tam giác ABC vuông tại A có .
• Ta đo độ dài các cạnh của tam giác ABC lần lượt là:
AB = 5 cm, AC = 4 cm và BC ≈ 6,4 cm.
• Từ các độ dài các cạnh đo được, ta có các tỉ số lượng giác của góc 40° như sau:
• Kiểm tra lại bằng máy tính, ta có:
sin 40° ≈ 0,64; cos 40° ≈ 0,77;
tan 40° ≈ 0,84; cot 40° ≈ 1,19.
Nhận xét: Tỉ số lượng giá sau khi vẽ hình, đo độ dài các cạnh và tính so với tính bằng máy tính cầm tay, ta thu được hai kết quả gần bằng nhau.
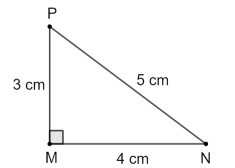
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm.
• Chẳng hạn tam giác MNP vuông có MP = 3 cm, MN = 4 cm, NP = 5 cm.
Ta có MP2 + MN2 = 32 + 42 = 52 = NP2.
Theo định lí Pythagore, ta có tam giác MNP vuông tại M.
• Các tỉ số lượng giác của góc N là:
• Vì tam giác MNP vuông tại M nên và là hai góc phụ nhau.
Khi đó, các tỉ số lượng giác của góc P là:
Dùng thước đo góc, ta có: .
Từ các tỉ số lượng giác ở trên, sử dụng máy tính cầm tay, ta thu được kết quả xấp xỉ kết quả khi đo góc.
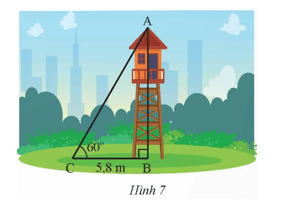
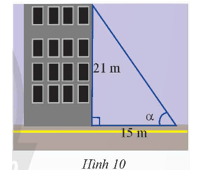
Tìm chiều cao của tháp canh trong Hình 7 (kết quả làm tròn đến hàng phần trăm).