Câu hỏi:
69 lượt xemXác định bậc của hai đa thức là tổng, hiệu của:
A(x) = -8x5 + 6x4 + 2x2 - 5x + 1 và B(x) = 8x5 + 8x3 + 2x - 3
Lời giải
Hướng dẫn giải:
- Ta có thể thực hiện A(x) + B(x) theo hai cách
Cách 1: Cộng theo cột dọc:
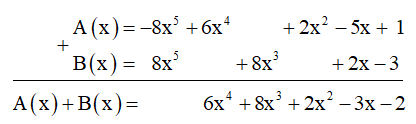
Cách 2: Cộng theo hàng ngang:
A(x) + B(x) = -8x5 + 6x4 + 2x2 - 5x + 1 + 8x5 + 8x3 + 2x - 3
= (-8x5 + 8x5) + 6x4 + 8x3 + 2x2 + (-5x + 2x) + (1 - 3)
= 6x4 + 8x3 + 2x2 - 3x - 2
Do đó A(x) + B(x) = 6x4 + 8x3 + 2x2 - 3x - 2
Vậy bậc của đa thức A(x) + B(x) là 4.
- Ta có thể thực hiện A(x) ‒ B(x) theo hai cách
Cách 1: Trừ theo cột dọc:
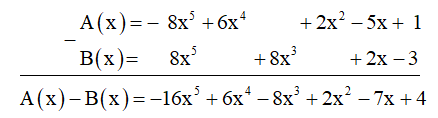
Cách 2: Trừ theo hàng ngang:
A(x) - B(x)
= -8x5 + 6x4 + 2x2 - 5x + 1 - (8x5 + 8x3 + 2x - 3)
= -8x5 + 6x4 + 2x2 - 5x + 1 - 8x5 - 8x3 - 2x + 3
= (-8x5 - 8x5) + 6x4 - 8x3 + 2x2 + (-5x - 2x) + (1 + 3)
= -16x5 + 6x4 - 8x3 + 2x2 - 7x + 4
Do đó A(x) - B(x) = -16x5 + 6x4 - 8x3 + 2x2 - 7x + 4
Vậy bậc của đa thức A(x) - B(x) là 5.
Tính tổng của hai đa thức sau bằng hai cách:
Q(x) = -8x3 + 4x2 + 6 + 3x
