Câu hỏi:
141 lượt xema) Giả sử G là một đồ thị với n đỉnh và ((?−1)(?−2))/2+2 cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.
b) Tìm một đồ thị với n đỉnh và ((?−1)(?−2))/2+1 cạnh mà không có chu trình Hamilton.
Lời giải
Hướng dẫn giải:
a) Định lí Ore: Nếu G là một đồ thị có n đỉnh (n ≥ 3) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.
Ta có lí thuyết: Giả sử G là đồ thị đơn gồm n đỉnh và m cạnh. Nếu m ≥ (?^2-3? +6)/2 thì G là đồ thị có chu trình Hamilton.
Áp dụng vào bài toán ta được điều phải chứng minh.
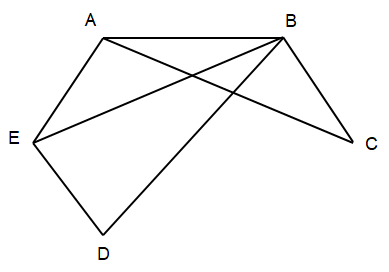
b) Ta có đồ thị sau có 5 đỉnh, 7 cạnh và đồ thị không có chu trình Hamilton.
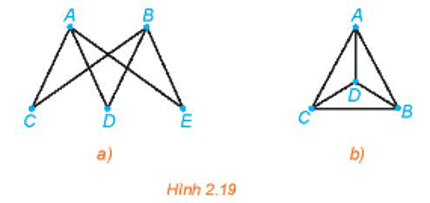
Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.