Câu hỏi:
38 lượt xemVới giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Euler? Có một đường đi Euler?
Lời giải
Hướng dẫn giải:
Đồ thị đầy đủ Kn có n ≥ 2, n ∈ ℕ.
Đồ thị đầy đủ Kn là đồ thị liên thông.
Mỗi đỉnh của Kn đều có bậc là n – 1.
+) Theo định lí Euler, Kn có chu trình Euler khi Kn liên thông (đã thỏa mãn) và mọi đỉnh của Kn đều có bậc chẵn, điều này có nghĩa để Kn có một chu trình Euler thì n – 1 phải là số chẵn hay n phải là số lẻ, tức là n = 2k + 1 (k ∈ ℕ*). Vậy với n = 2k + 1 (k ∈ ℕ*) thì đồ thị đầy đủ Kn có một chu trình Euler.
+) Đồ thị Kn có một đường đi Euler từ A đến B khi và chỉ khi Kn liên thông và mọi đỉnh của Kn đều có bậc chẵn, chỉ trừ A và B có bậc lẻ. Mà mọi đỉnh của Kn đều có bậc là n – 1, nghĩa là mọi đỉnh của Kn đều có bậc chẵn hoặc đều có bậc lẻ.
- Với n = 2, ta có K2 có 2 đỉnh đều có bậc là 1 (là bậc lẻ) nên ta có đường đi Euler từ đỉnh này qua đỉnh còn lại.
- Với n > 2, n ∈ ℕ* thì mọi đỉnh của Kn đều có bậc cùng chẵn hoặc cùng lẻ lớn hơn 2, do đó không thỏa mãn điều kiện để Kn có đường đi Euler.
Vậy đồ thị đầy đủ Kn có một đường đi Euler khi n = 2.
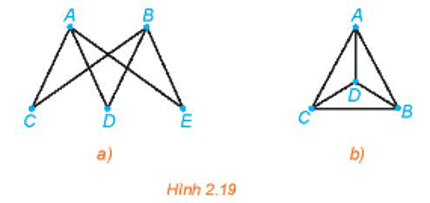
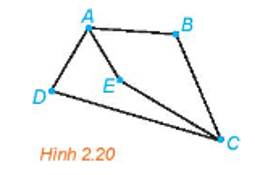
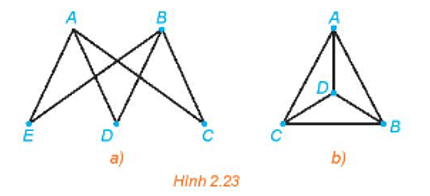
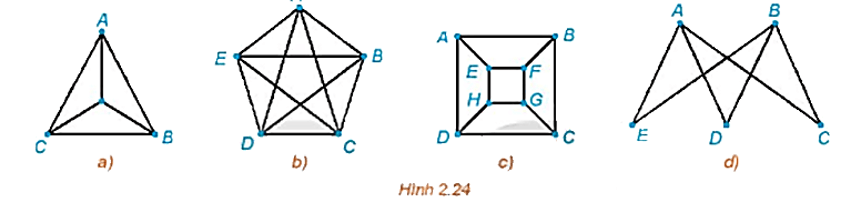
Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
Có thể nào đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?
Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 78 lượt thi