Câu hỏi:
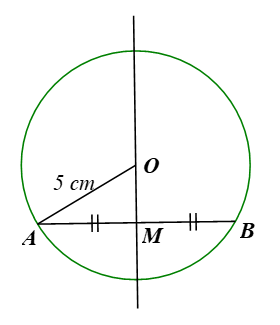
109 lượt xemCho đường tròn (O; R) và dây AB khác đường kính. Gọi M là trung điểm của AB.
a) Đường thẳng OM có phải là đường trung trực của đoạn thẳng AB hay không? Vì sao?
b) Tính khoảng cách từ điểm O đến đường thẳng AB, biết R = 5 cm, AB = 8 cm.
Lời giải
Hướng dẫn giải:
a) Vì AB là dây cung của đường kính (O; R) nên ta có OA = OB = R.
Khi đó, O nằm trên đường trung trực của AB.
Lại có M là trung điểm của AB nên M cũng nằm trên đường trung trực của AB.
Do đó OM là đường trung trực của đoạn thẳng AB.
b) Vì M là trung điểm của AB nên ta có MA = MB = AB2=82��2=82 = 4 (cm).
Vì OM là đường trung trực của đoạn thẳng AB nên OM ⊥ AB hay ∆OAM vuông tại M.
Theo định lí Pythagore ta có: OA2 = OM2 + AM2
Suy ra OM2 = OA2 – AM2 = 52 – 42 = 9.
Do đó OM = 3 cm.
Vậy khoảng cách từ điểm O đến đường thẳng AB là 3 cm.
Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm của hình đó.