Câu hỏi:
63 lượt xem Tự luận
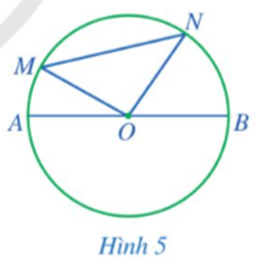
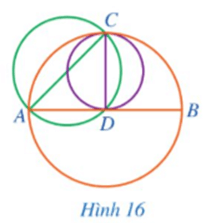
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.
Lời giải
Hướng dẫn giải:
Nối OM, ON.
Xét ∆OMN, ta có: MN < OM + ON (Bất đẳng thức tam giác). (1)
Vì B, M, N, C cùng thuộc đường tròn (O) nên OA = OM = ON = OB.
Ta có: OM + ON = OB + OC.
Lại có BC là đường kính của đường tròn (O) nên BC = OB + OC.
Do đó OM + ON < BC. (2)
Từ (1) và (2) suy ra MN < AB.
Câu 1:
Câu 2:
Câu 3:
Tự luận
Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.
1 năm trước
53 lượt xem
Câu 4:
Câu 6:
Câu 8:
Tự luận
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm của hình đó.
1 năm trước
51 lượt xem
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Câu 16:
Câu 17:
Câu 18:
Câu 19:
Câu 20:
Câu 21: