Câu hỏi:
360 lượt xem Tự luận
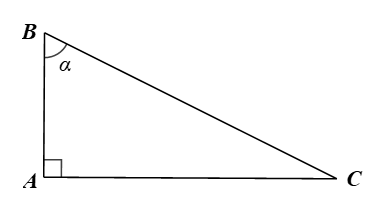
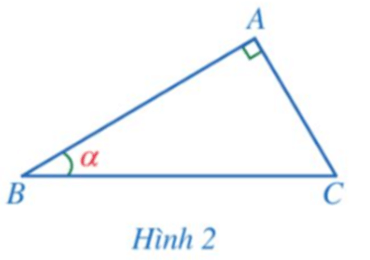
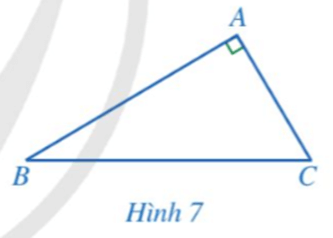
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.
b) Chứng minh:
Từ đó, tính giá trị biểu thức: S = sin235° + cos235°; T = tan61°.cot61°.
Lời giải
Hướng dẫn giải:
a) Xét ∆ABC vuông tại A, ta có:
sin = sinB = ; cos = cosB = ;
tan = tanB = ; cot = cotB = .
b) Xét ∆ABC vuông tại A, ta có:
⦁ BC2 = AB2 + AC2 (định lí Pythagore);
⦁
⦁
⦁
⦁ cot.tan = = 1.
Ta có: S = sin235° + cos235° = 1; T = tan61°.cot61° = 1.
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
 trên máy tính cầm tay. Trước hết, ta đưa máy tính về chế độ “độ”. Để nhập độ, phút giây, ta sử dụng phím
trên máy tính cầm tay. Trước hết, ta đưa máy tính về chế độ “độ”. Để nhập độ, phút giây, ta sử dụng phím  .
.