Câu hỏi:
124 lượt xemBài toán: Tìm đa thức P sao cho A = B . P, trong đó
A = 2x4 - 3x3 - 3x2 + 6x - 2 và B = x2 - 2
Lời giải
Hướng dẫn giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Thực hiện theo các bước sau:
Bước 1: Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B:
2x4 : x2 = 2x2.
Bước 2: Lấy A trừ đi tích B . 2x2 ta được dư thứ nhất là -3x3 + x2 + 6x - 2.
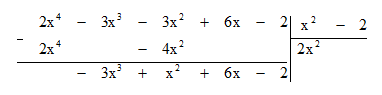
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B:
(-3x3) : x2 = -3x.
Bước 4: Lấy dư thứ nhất trừ đi tích B . (-3x) ta được dư thứ hai là x2 - 2.
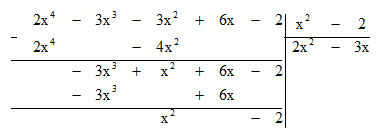
Bước 5: Lấy hạng tử bậc cao nhất của dư thứ hai chia cho hạng tử bậc cao nhất của B:
x2 : x2 = 1.
Bước 6: Lấy dư thứ hai trừ đi tích B . 1 ta được dư thứ ba là 0.
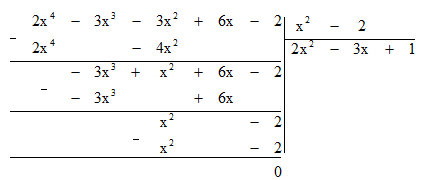
Dư cuối cùng bằng 0 nên quá trình chia kết thúc.
Vậy A : B = 2x2 - 3x + 1.
Tìm thương của mỗi phép chia hết sau:
a) 12x3 : 4x; b) (-2x4) : x4; c) 2x5 : 5x2
Thực hiện các phép chia sau:
a) 3x7 : x4; b) (-2x) : x; c) 0,25x5 : (-5x2)
Thực hiện phép chia:
a) (-x6 + 5x4 - 2x3) : 0,5x2.
b) (9x2 - 4) : (3x + 2)
Tính:
a) 8x5 : 4x3; b) 120x7 : (-24x5);
c) (-x)3 : x d) -3,72x4 : (-4x2)
