Câu hỏi:
72 lượt xemTrong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:
F(x) = G(x) . Q(x) + R(x).
a) F(x) = 6x4 - 3x3 + 15x2 + 2x - 1; G(x) = 3x2.
b) F(x) = 12x4 + 10x3 - x - 3; G(x) = 3x2 + x + 1
Lời giải
Hướng dẫn giải:
a) Đặt tính chia như sau:
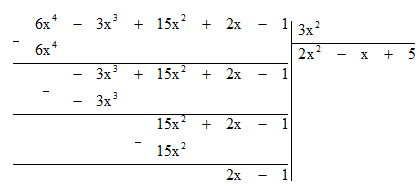
Do đó Q(x) = 2x2 - x + 5; R(x) = 2x - 1.
Vậy 6x4 - 3x3 + 15x2 + 2x - 1 = 3x2 . (2x2 - x + 5) + 2x - 1.
b) Đặt tính chia như sau:
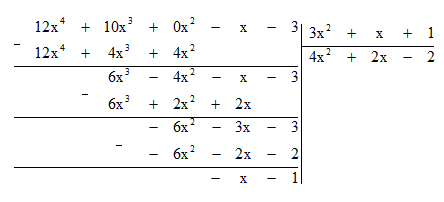
Do đó Q(x) = 4x2 + 2x - 2; R(x) = -x - 1.
Vậy 12x4 + 10x3 - x - 3 = (3x2 + x + 1) . (4x2 + 2x - 2) - x - 1.
Tìm thương của mỗi phép chia hết sau:
a) 12x3 : 4x; b) (-2x4) : x4; c) 2x5 : 5x2
Thực hiện các phép chia sau:
a) 3x7 : x4; b) (-2x) : x; c) 0,25x5 : (-5x2)
Thực hiện phép chia:
a) (-x6 + 5x4 - 2x3) : 0,5x2.
b) (9x2 - 4) : (3x + 2)
Tính:
a) 8x5 : 4x3; b) 120x7 : (-24x5);
c) (-x)3 : x d) -3,72x4 : (-4x2)
