Câu hỏi:
89 lượt xem Tự luận
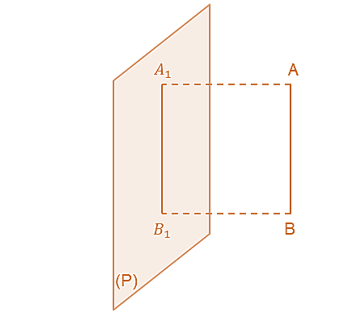
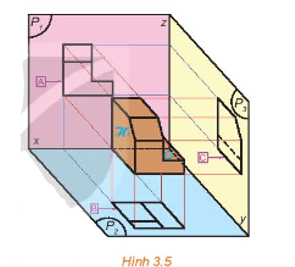
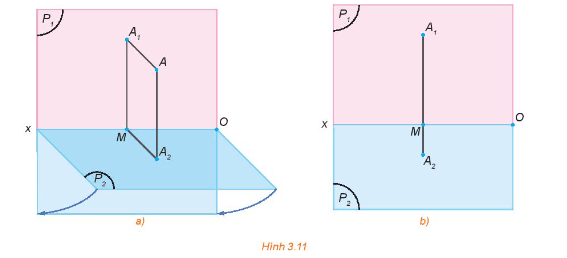
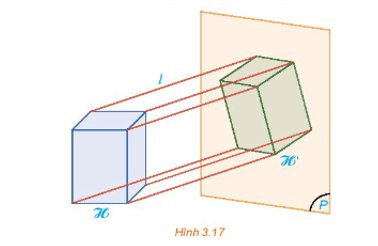
Cho đoạn thẳng AB và gọi A1B1 là hình chiếu đứng của AB. Biết đường thẳng AB song song với mặt phẳng hình chiếu đứng, chứng minh rằng AB = A1B1.
Lời giải
Hướng dẫn giải:
Từ A, B kẻ các đường thẳng vuông góc với mặt phẳng hình chiếu đứng (P). Đường thẳng qua A và B lần lượt giao với mặt phẳng (P) tại các điểm A1, B1.
Ta có: AA1 // BB1 (vì AA1, BB1 cùng vuông góc với (P))
Vì AB // (P) nên khoảng cách từ A đến (P) bằng khoảng cách từ B đến (P).
Hay AA1 = BB1.
Do đó, tứ giác AA1B1B là hình bình hành.
Suy ra: AB = A1B1.
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Tự luận
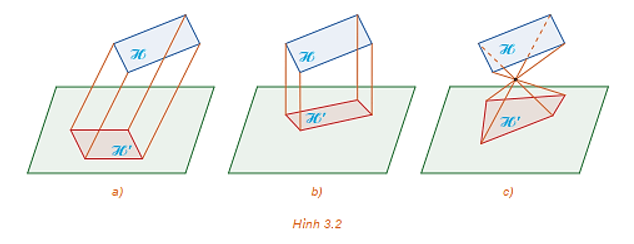
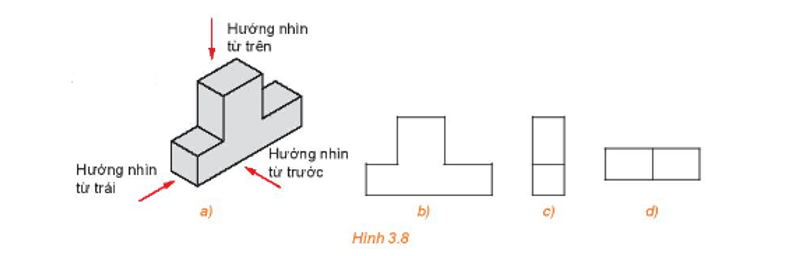
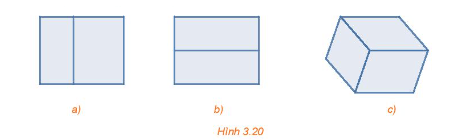
Xác định hình chiếu vuông góc của hình ℋ (H.3.8a) trong các hình dưới đây.
1 năm trước
106 lượt xem
Câu 6:
Câu 7:
Câu 10:
Câu 12:
Câu 13:
Câu 15:
Câu 16:
Câu 17:
Câu 19:
Câu 21:
Câu 22:
Câu 23:
Câu 25:
Câu 26:
Câu 27:
Câu 28:
Câu 30:
Câu 31:
Câu 32:
Câu 33: