Câu hỏi:
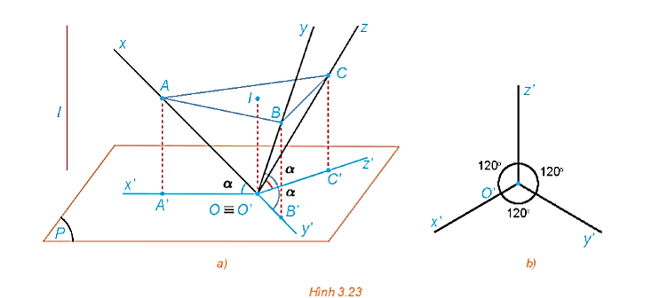
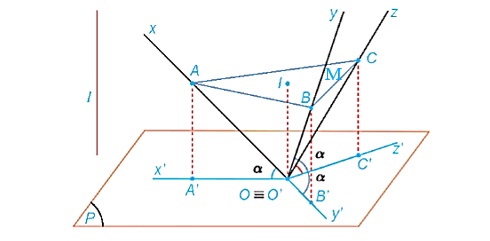
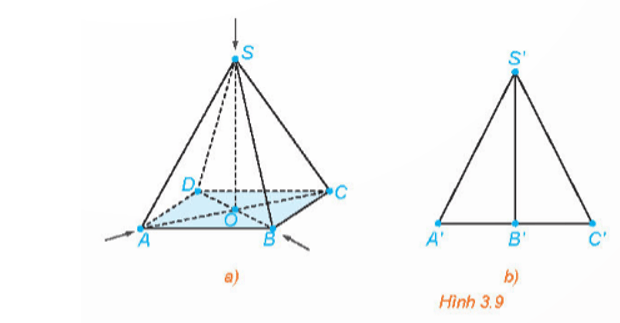
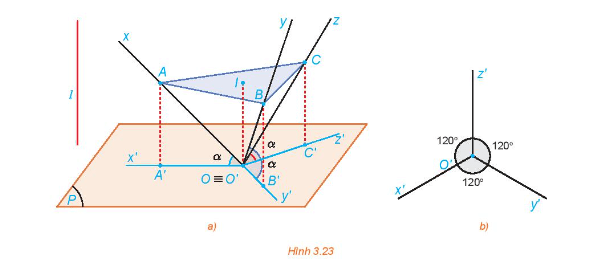
102 lượt xemTrong HĐ7, bằng cách xét tam giác vuông OIA và tính tỉ số ??/?? , chứng minh rằng trong phép chiếu trục đo vuông góc đều thì p = q = r = √6/3 .
Lời giải
Hướng dẫn giải:
Gọi M là trung điểm của BC.
Ta có: O.ABC là hình chóp tam giác đều nên OA = OB = OC.
Vì I là tâm tam giác đều ABC nên . (1)
Tam giác OBC vuông cân tại O nên OM vừa là đường cao, vừa là đường phân giác, vừa là đường trung tuyến.
Suy ra ??=1/2 ?? hay 2OM = BC.
Tam giác vuông cân OBC có 2OB2 = BC2.
Do đó: 2OB2 = 4OM2. Suy ra OM2 = 1/2 OA2. (2)
Tam giác OIM vuông tại I có: OI2 + IM2 = OM2. (3)
Mà OI2 = OA2 – IA2 (tam giác OIA vuông tại I) (4)
Thay (1), (2), (4) vào (3) ta được:
OA mũ 2 − IA mũ 2+1/4 IA mũ 2=1/2 OA mũ 2
Suy ra IA mũ 2 / OA mũ 2 = 2/3 nên IA/OA=√6/3.
Mà IA = O'A' (do AIO'A' là hình bình hành).
Do đó, p = q = r = O'A'/OA=√6/3.
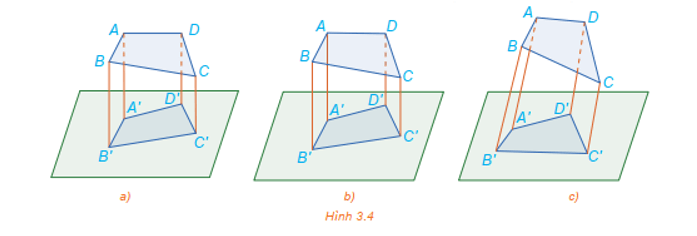
Quan sát Hình 3.4 và cho biết hình nào thể hiện hình chiếu trục đo của tứ giác ABCD.
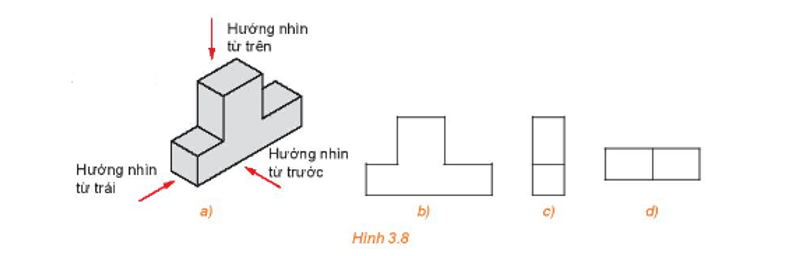
Xác định hình chiếu vuông góc của hình ℋ (H.3.8a) trong các hình dưới đây.