Câu hỏi:
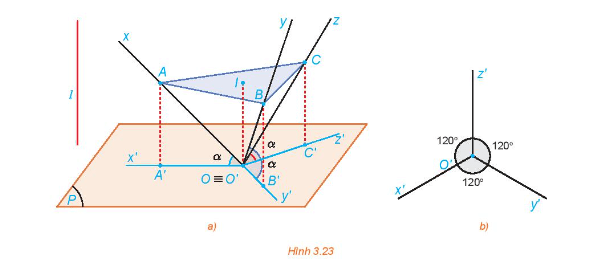
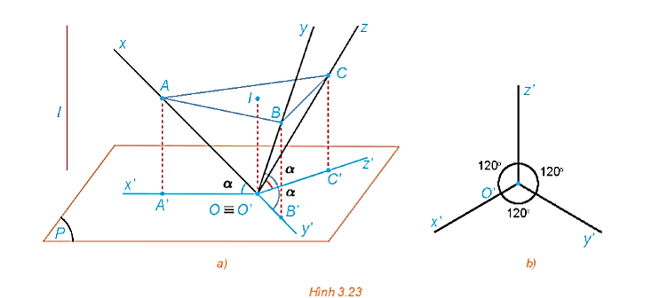
125 lượt xemCho hình tứ diện vuông OABC có các cạnh OA, OB, OC bằng nhau và lần lượt nằm trên các trục Ox, Oy, Oz đôi một vuông góc. Xét phép chiếu vuông góc lên mặt phẳng (P) đi qua O sao cho các trục Ox, Oy, Oz tạo với (P) các góc bằng nhau (H.3.23a). Gọi A', B', C' lần lượt là hình chiếu của A, B, C.
a) Chứng minh rằng ABC là tam giác đều.
b) Giải thích tại sao các khoảng cách từ A, B, C đến (P) bằng nhau, từ đó suy ra mặt phẳng (ABC) song song với mặt phẳng (P).
c) Gọi I là tâm tam giác đều ABC. Giải thích tại sao góc A'OB'= góc AIB, từ đó suy ra góc A'O'B'= góc B'O'C'= góc A'O'C'=120°.
Lời giải
Hướng dẫn giải:
a) Ta có: OA = OB = OC, góc AOB = góc BOC = góc COA = 90°.
Suy ra các tam giác AOB, BOC và COA bằng nhau từng đôi một.
Từ đó suy ra AB = BC = CA nên tam giác ABC là tam giác đều.
b) Ta có: OA = OB = OC; góc AA'O = góc BB'O = góc CC'O = 90°; góc AOA' = góc BOB' = góc COC' = α.
Do đó, các tam giác AA'O, BB'O và CCO' bằng nhau từng đôi một.
Từ đó suy ra AA' = BB' = CC'.
Do đó, khoảng cách từ A, B, C đến (P) bằng nhau.
Ta có: AA' = BB', AA' // BB' nên ABB'A' là hình bình hành.
Suy ra: AB // A'B'.
Tương tự ta chứng minh BC // B'C'; CA // C'A'
Mà A'B', B'C', C'A' thuộc (P)
Suy ra: (ABC) song song với (P).
c) Dễ dàng chứng minh được IA = O'A' (AIO'A' là hình bình hành).
Tương tự IB = O'B', AB = A'B'.
Do đó ∆IAB = ∆O'A'B' (c.c.c).
Suy ra góc A'O'B' = góc AIB.
Tương tự, ta chứng minh được góc A'O'C' = góc CIA; góc B'O'C' = góc BIC.
Do I là tâm tam giác đều ABC nên dễ dàng chứng minh được góc AIB = góc BIC = góc CIA = 120°.
Nên suy ra góc AIB = góc BIC = góc CIA = góc A'O'B' = góc B'O'C'= góc A'O'C'.
Vậy góc A'O'B' = góc B'O'C' = góc A'O'C' = 120°.
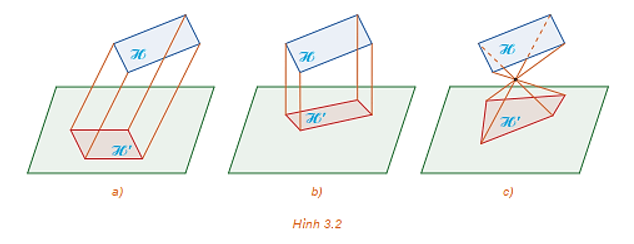
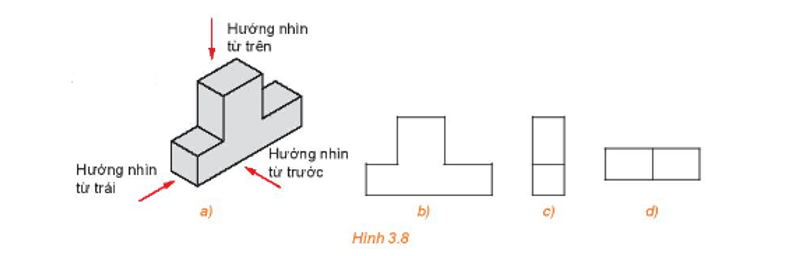
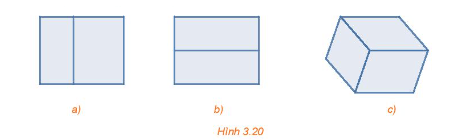
Xác định hình chiếu vuông góc của hình ℋ (H.3.8a) trong các hình dưới đây.