Câu hỏi:
152 lượt xem Tự luận
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song.
Lời giải
Hướng dẫn giải:
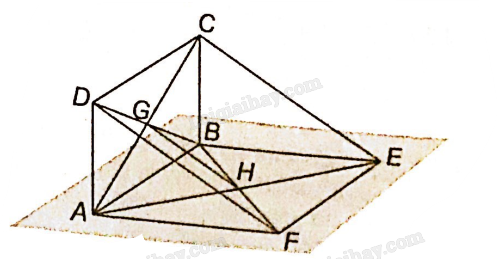
G là giao điểm hai đường chéo BD, AC của hình bình hành ABCD nên G là trung điểm của BD và AC.
H là giao điểm hai đường chéo BF, AE của hình bình hành ABEF nên H là trung điểm của BF và AE.
Xét tam giác BDF, GH là đường trung bình của tam giác nên GH song song với DF.
GH là đường trung bình tam giác ACE nên GH song song với CE.
Vậy ba đường thẳng GH, CE, DF đôi một song song.
Câu 1:
Câu 2:
Câu 3:
Câu 7:
Câu 8: