Câu hỏi:
93 lượt xem Tự luận
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng sau điểm A, B, C, D, E, F là sáu đỉnh của một hình lăng trụ tam giác.
Lời giải
Hướng dẫn giải:
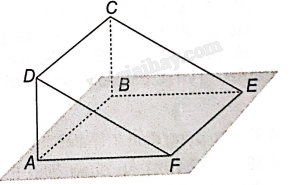
Vì AD//BC (do ABCD là hình bình hành) nên AD//mp (BCE), AF//BE (do ABEF là hình bình hành) nên AF//mp (BCE).
Mà AD và AF là hai đường thẳng cắt nhau cùng nằm trong mặt phẳng ADF. Do đó, mp (ADF) //mp (BCE).
Các đường thẳng AB, CD, EF đôi một song song với nhau.
Câu 2:
Câu 4:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 11:
